Marco Fumagalli

La part horaire, véritable horoscope lunaire

Phos 2, Juin 2001.
Traduction de Danièle Jay,
Le Grès, 13 juillet 2009

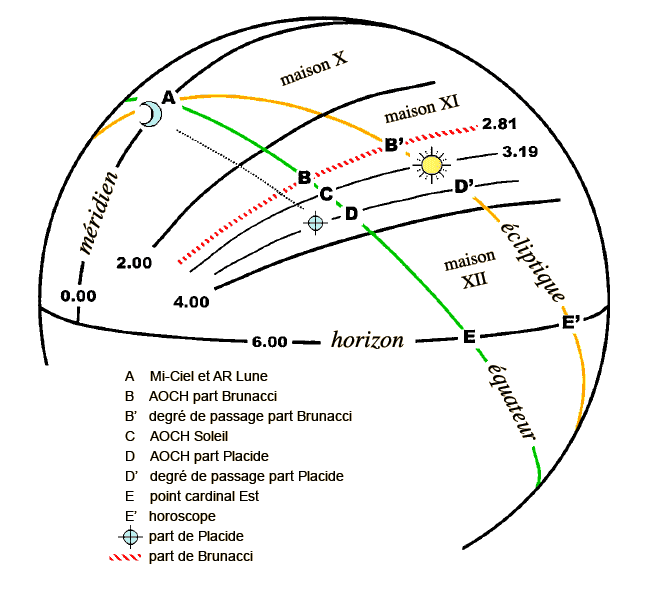
Le calcul des parts est l’un des sujets les plus complexes et les plus controversés de toute la théorie astrologique. La méthode exposée par Placide dans le «Canon de la part de fortune», à la fin de son traité sur le Primum Mobile (1657), peut certainement être définie comme une méthode in mundo, car elle repose sur les arcs d’équateur, et non pas sur les simples distances écliptiques de la méthode «vulgaire». La méthode, comme il nous le dit lui-même, lui fut présentée par son ami Adriano Negusanzio, «homme très versé dans la discipline astrologique selon la doctrine authentique de Ptolémée». Negusanzio se rendit compte du caractère inapproprié de la méthode vulgaire, qui ne reposait que sur les coordonnées célestes du Soleil et de la Lune, la situation locale des deux astres n’étant pas prise en compte. Il imagina alors un autre système qui répondît mieux au principe bien connu de Ptolémée:

«La part de fortune doit être calculée, et le jour et la nuit, en comptant le nombre de degrés séparant le Soleil de la Lune, et en reportant cette même distance à partir de l’horoscope dans le sens des signes, de telle sorte que le rapport et la configuration du Soleil vis-à-vis de l’horoscope soient aussi ceux de la Lune vis-à-vis de la part de fortune, celle-ci apparaissant comme un horoscope lunaire» (Tetr. III, 11). 

 Résumons brièvement la méthode de Negusanzio-Placide, que nous avons exposée de façon complète dans l’article «Le calcul des parts selon Placide». Le principe est le suivant: là où se trouve la Lune quand le Soleil est à l’horoscope, là est le lieu de la part. Pour trouver la position de la part, Negusanzio calcule en ascension oblique la distance entre le Soleil et l’horoscope, et lui ajoute l’ascension droite de la Lune. Il obtient ainsi l’ascension droite de la part, qui se trouvera toujours sur le même parallèle de déclinaison que la Lune.

AR () = AO (Hor) - AO () + AR ()

Si nous appliquons ce calcul pour le moment du lever du Soleil, nous trouverons que l’ascension droite de la part correspond à celle de la Lune. En plaçant la part de fortune sur le parallèle de la Lune, nous aurons une correspondance totale entre la Lune et la part: celle-ci aura une distance horaire vis-à-vis de la Lune identique à celle de l’horoscope vis-à-vis du Soleil, c'est-à-dire égale à zéro. Nous pouvons donc dire que cette part est l’horoscope lunaire.

Limites de la méthode Negusanzio-Placide

Cette méthode répond donc parfaitement au principe ptoléméen, mais seulement lorsque le Soleil se lève. En fait, dès que le Soleil commence à monter au-dessus de l’horizon dans le mouvement diurne, la Lune elle aussi se déplace et leur distance horaire prend des valeurs différentes. La part placidienne au contraire reste à peu près immobile dans le lieu où elle se trouvait au lever du Soleil, se déplaçant seulement légèrement, en vertu du mouvement de la Lune en ascension droite. Ce qui signifie que pendant la rotation diurne la part de Placide n’entretient plus vis-à-vis de la Lune le même rapport horaire qu’a le Soleil vis-à-vis de l’horoscope, et cesse par conséquent d’être l’horoscope lunaire. Démontrons ce qui vient d’être dit sur un exemple:

figure 1	figure 2

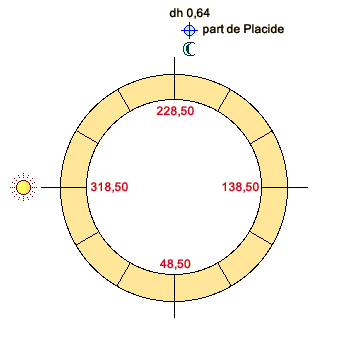
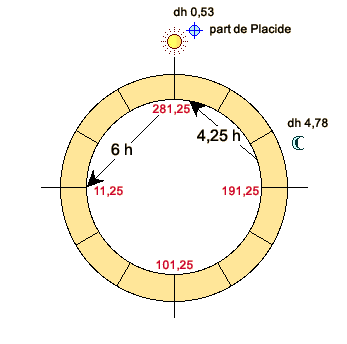
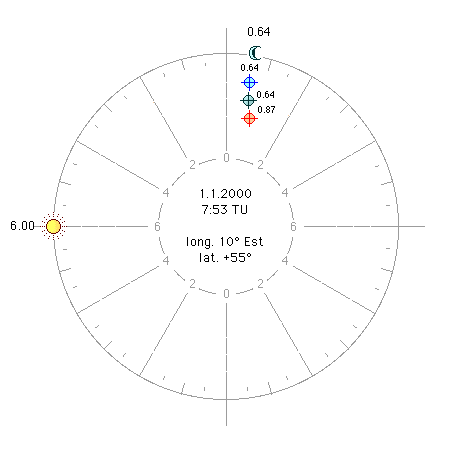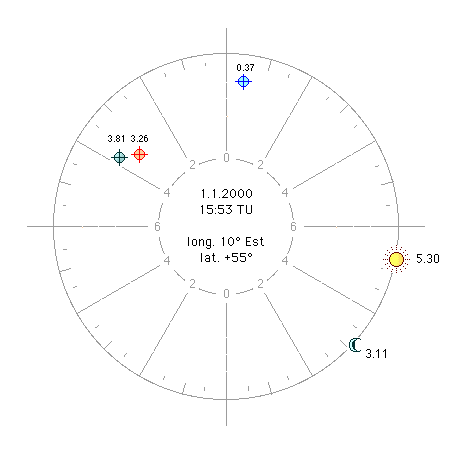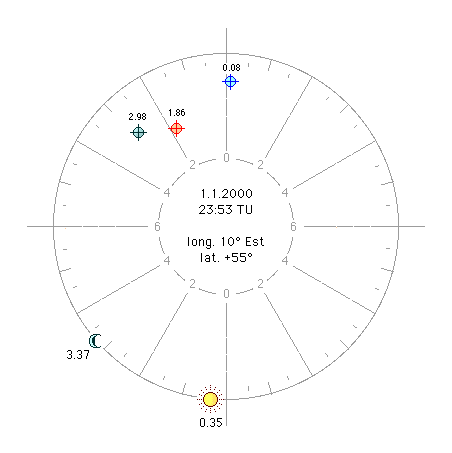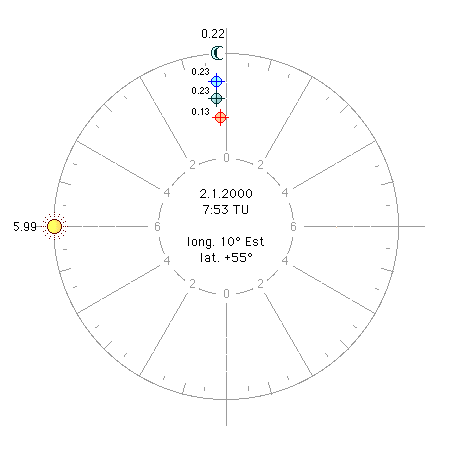
a1) Soleil à l’horoscope (figure 1). Prenons le thème suivant: 1^er janvier 2000, 7h 52mn 51s TU, pôle +55°, long. 10° Est. Le 20°56’ Scorpion culmine. ARMC 228°,50. Le centre du Soleil est en train de se lever (hauteur = 0°). Sa longitude est la même que celle de l’horoscope: 10°12’ Capricorne. Son ascension oblique (AO) est la même que celle de l’horoscope (AOHOR 318°,50). La Lune est à 11°15’ Scorpion. Sa latitude est de +5°,20. Elle est en maison IX, à une distance horaire du MC de 0,64 h. Son ascension droite (AR) est de 220°,46. Sa déclinaison de –10°,26. Nous sommes maintenant en mesure de calculer la part lunaire avec la méthode de Placide:

AR () = 318,50 – 318,50 + 220,46 = 220,46

En assignant à la part la déclinaison de la Lune, -10°,26, nous trouvons que la part est distante du MC de 0,64 h, en maison IX, et qu’elle est distante de l’horoscope de 6,64 h. La correspondance est parfaite.

a2) Soleil loin de l’horoscope (figure 2). Avançons-nous maintenant dans le temps, par exemple jusqu’à 11h 23mn 15s TU, heure à laquelle le Soleil culmine. Le 10°20’ Capricorne culmine. ARMC 281°,25. Le 0°27’ Taureau se lève. AOHOR 11°,25. La longitude du Soleil est la même que celle du MC, 10°,20 Capricorne. Son AO est de 318°,64 (degré d’équateur qui se lève avec le 10°,20 Capricorne au pôle +55°). La Lune est à 13°,01 Scorpion. Sa latitude est de +5°,18. Sa déclinaison de –10°,80, en maison VII, à une distance horaire du MC de 4,78 h. Son ascension droite (AR) est de 222°,15. Ses heures temporelles diurnes de 12°,36. Du fait que le Soleil culmine, la distance horaire de ce dernier est de 0. Les deux luminaires ont donc entre eux une distance de 4,78 h. Le Soleil est à une distance de l’horoscope de 6 h, et donc nous devrons nous attendre à un horoscope lunaire à 6h de la Lune. Voyons si tel est le cas:

AR () = 11°,25 (+360°) – 318°,64 + 222°,15 = 274°,76

Du fait que la déclinaison et les heures temporelles de la part sont celles de la Lune, prenons la distance méridienne de la part, ARMC – AR part = 6°,49. Divisons-la par les heures temporelles diurnes 12°,36. Nous obtenons 0,53 h, distance horaire de la part en maison IX. La distance horaire entre la part de Placide et la Lune est seulement de 4,25 h, valeur bien inférieure aux 6 h que nous attendions. Nous ne pouvons certainement pas dire que nous avons trouvé l’horoscope lunaire dont parle Ptolémée!

Que s’est-il passé? Il s’est passé que cette part, calculée sur la base des ascensions obliques au pôle de la région, est restée presque immobile (en réalité elle s’est déplacée légèrement parce que l’ascension droite de la Lune a un peu bougé), alors que la distance horaire entre les deux luminaires a par contre notablement changé. Donc, si nous cherchons le véritable horoscope lunaire, nous devrons adopter une méthode qui tienne compte de ce déplacement: nous devrons adopter une méthode horaire.

Le véritable horoscope lunaire

Quelques années après la mort de Placide, lors de la ré-impression de la  Coelestis Philosophia de 1675, Francesco Brunacci et Francesco Maria Onorati s’avisèrent du caractère inapproprié de la méthode placidienne et en proposèrent une nouvelle. Il s’agit de la méthode horaire. Brunacci et Onorati ne parlent pas expressément d’heures mais de distances équatoriales, ce qui nous le savons est la même chose. Le calcul conserve la même structure mais il est fait entièrement sur l’équateur en utilisant l’ascension oblique de l’horoscope et les ascensions mixtes (AM) des luminaires, c'est-à-dire les AOCH dans l’hémisphère ascendant et les DOCH dans l’hémisphère descendant. Ce que nous obtenons est à son tour l’ascension mixte de la part:

AM () = AO (Hor) - AM () + AM ()

Appliquons maintenant cette méthode à notre exemple du 1er janvier 2000 à 7h 52mn 51s TU (voir plus haut):

figure 3	figure 4

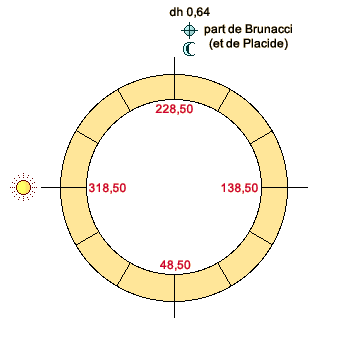
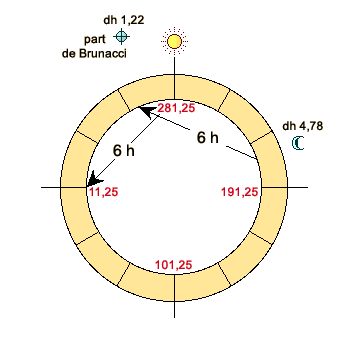
 b1) Soleil à l’horoscope (figure 3). L’ascension mixte du Soleil (dans ce cas il s’agit d’une ascension oblique à son propre pôle, AOCH) est identique à l’ascension oblique de l’horoscope (AOHOR), 318°,50, du fait que le Soleil se lève et que son pôle est de +55°, comme celui de la région. Le pôle de la Lune est de 9°,37 et son ascension mixte de 218°,85. Du fait que la Lune est dans l’hémisphère descendant (elle vient juste de passer le méridien), il s’agit d’une descension oblique (DOCH), au pôle 9°,37. Nous avons alors: 

AM () = 318°,50 – 318°,50 + 218°, 85 = 218°,85

Nous voyons immédiatement que cette valeur est identique à la DOCH de la Lune. Prenons la distance de ce point au méridien (ARMC – 218°,85), nous obtenons un arc de 9°,65 qui, divisé par 15, correspond à une distance du méridien de 0,64 h en maison IX. La part coïncide à nouveau parfaitement avec la Lune. Donc, lorsque le Soleil se lève, nous obtenons le même résultat qu’avec la méthode de Negusanzio-Placide. La figure 3 répond à la figure 1. 

b2) Soleil loin de l’horoscope (figure 4). Lorsque le Soleil culmine, son AOCH est de 281°,25. Elle est identique à son ascension droite puisque le Soleil se trouve au méridien dont le pôle est 0°. Le pôle de la Lune est de 49°,47 et son ascension mixte (AM) de 209°,55. Du fait que la Lune est dans l’hémisphère descendant, il s’agit d’une descension oblique (DOCH) au pôle 49°,47.

AM () = 11°,25 (+360°) – 281°,25 + 209°,55 = 299°,55

Cette valeur est supérieure à l’ARMC, ce qui signifie que nous sommes en maison X et non plus en maison IX. Prenons alors la distance entre ce degré d’équateur et le méridien (299°,55 – ARMC): nous obtenons un arc de 18°,30 qui, divisé par 15, donne une distance horaire de 1,22 h en maison X. La Lune est en maison VII, à 4,78 h du MC et du Soleil. Si nous ajoutons la distance horaire de la Lune en VII et la distance horaire de la part en X (1,22 h), nous voyons que la distance horaire entre la Lune et la part est exactement de 6 h, tout comme la distance du Soleil à l’horoscope. Nous avons trouvé le véritable horoscope lunaire. La figure 4 répond à la figure 2: la part «horaire» de Brunacci est distante d’1 bonne heure,75 de celle de Placide.

Nous pouvons procéder de la même façon avec toutes les autres parts, en prenant toujours les ascensions du point qui monte, et les descensions de celui  qui descend.

Le degré de passage

La méthode «horaire» de Brunacci et Onorati comporte une différence dans la façon de repérer le degré de passage de la part, c'est-à-dire le degré qui passe à la même distance horaire que celle de la part et qui peut être pris comme référence pour l’attribution des dignités planétaires. Rappelons en premier lieu comment on trouve le degré de passage de la part placidienne.

a) la part de Placide. Avec la méthode de Placide on doit procéder en attribuant à la part la déclinaison et la différence ascensionnelle (DA) de la Lune, en appliquant la formule des pôles qui répartit la différence ascensionnelle selon la distance horaire de la part (DH):

tg P = sin (1/6 DA. DH) . cotg déc.

Dans notre exemple (a2) nous obtiendrons le résultat suivant, connaissant la déclinaison (déc) de la part (-10°,80), sa DA (15°,82) et sa DH (0,53 h):

tg P = sin (1/6 15,82 . 0,53) . cotg (-10°,80)

P = 7°,29

Nous pouvons maintenant trouver le degré de passage (thêta) avec les tables des pôles (ou avec la formule habituelle que nous utilisons aussi pour les cuspides des maisons), en calculant d’abord la DOCH de la part (elle se trouve en maison IX, donc dans l’hémisphère descendant), DOCH que nous ne connaissons pas encore: DOCH part = ARMC – 15. DH = 273°,3.

 Procédons alors avec la formule:

Nous trouvons que thêta est égal à 275°,93 ce qui fait 5°56’ Capricorne. C’est le degré écliptique qui passe à la même distance horaire que celle de la part de Placide (pour ce calcul, on pourra aussi consulter l’article «le calcul des parts selon Placide»).

b) la part horaire. Avec la méthode horaire nous ne pouvons pas attribuer à la part la déclinaison de la Lune, ou plutôt nous ne pouvons lui attribuer aucune déclinaison. En fait, la part horaire n’est pas un point de la sphère (doté d’une ascension droite et d’une déclinaison), mais plutôt un cercle iso-horaire, une distance mesurée selon le mouvement des heures (voir figure 5). Elle y est en tout semblable à un horizon: nous pouvons la définir comme un horizon relatif à la Lune, un horoscope lunaire précisément. De même que tous les points de l’horizon sont à une même distance du Soleil exprimée en heures, de la même façon tous les points de l’horizon relatif à la Lune, c'est-à-dire tous les points de la part, sont à une même distance horaire de la Lune. Pour trouver le pôle de la part, nous pourrons alors choisir un point quelconque de ce cercle, par exemple celui qui est situé sur l’équateur ou sur l’écliptique, et nous pourrons opérer selon sa déclinaison et sa différence ascensionnelle.

Mais il existe une méthode plus élégante et plus simple, qui ne nous contraint pas à un choix arbitraire. Encore une fois, la méthode est exposée par Brunacci et Onorati: elle consiste à calculer le pôle de la part en considérant sa position en maison, selon sa distance proportionnelle des cuspides. C'est-à-dire, si par exemple le cercle de la part est en maison X et si nous connaissons sa distance horaire, sachant qu’une maison a une amplitude horaire de 2 h (ou 30° d’équateur), nous pouvons calculer le pôle (P) de la part en utilisant la proportion suivante:

P () = P1 +

(P2 - P1) . dp1 2

où P1 et P2 sont les pôles des cuspides de la maison où se trouve la part: P1 est celui qui a la valeur inférieure, P2 celui qui a la valeur supérieure; (P2 – P1) est l’amplitude polaire de la maison où se trouve la part; dp1 représente la distance horaire de la part à la cuspide la plus proche du méridien.

Appliquons cette méthode à l’exemple b2. Du fait que la part est en maison X, P1 correspond au pôle du méridien c'est-à-dire à 0°. P2 est le pôle de la cuspide de la maison XI, 26°,98. La part a une distance horaire de 1,22 h par rapport à P1.

P () = 0° +

(26,98 - 0) . 1,22 2

P() = 16.46

Une fois trouvé le pôle de la part, cherchons dans les tables des pôles quel degré correspond à l’ascension oblique de 299°,55 au pôle de 16°,46. Ou utilisons la formule:

Nous trouvons que thêta est égal à 291°,05 ce qui fait 21°03’ Capricorne.

Conclusion

Après avoir montré comment les deux calculs aboutissent à des résultats très différents entre eux, nous pouvons maintenant réfléchir sur la nature différente de ces deux parts. Toutes deux naissent de distances calculées sur des arcs d’équateur, mais la part de Placide a une ascension droite et une déclinaison (celles de la Lune), elle est donc un point précis de la sphère locale, tandis que celle de Brunacci est un cercle iso-horaire qui garde avec la Lune la même distance qu’a l’horizon avec le Soleil; par conséquent cette part est comme un véritable horoscope lunaire, un horizon relatif à la Lune. Brunacci exprime très clairement ce concept:

«La part de fortune ne doit pas être rapportée à la déclinaison de la Lune, mais au cercle iso-horaire sur lequel tombe le calcul, parce qu’elle doit être comme un horoscope lunaire. En fait nous considérons l’horizon du Soleil non pas comme le point où il se lève, mais comme un cercle dont le tracé émerge avec le degré du zodiaque, comme c’est le cas des constellations qui se lèvent avec lui. De la même façon, le degré du zodiaque qui coupe le cercle iso-horaire de la part selon les règles des ascensions obliques doit être placé dans le thème pour pouvoir en extraire le gouverneur de la vie, selon ce qu’enseigne Ptolémée».

La part horaire de Brunacci et Onorati sera donc adoptée comme véritable horoscope lunaire et la méthode sera étendue à toutes les autres parts. La différence entre les deux méthodes est substantielle et comporte quelques conséquences très importantes, en premier lieu dans l’usage des directions: 

a)   Comme nous l’avons vu, le calcul de Placide maintient le rapport horaire lorsque le Soleil se lève, et à ce moment-là il fixe la part en un point précis de la sphère qui correspond à la position de la Lune; à partir de cet instant la part reste fixe, comme un reflet immobile de la Lune sur ce point, qui se déplace seulement selon le mouvement lunaire lui-même en ascension droite. Ce qui signifie que la part est considérée comme un astre ayant ses propres coordonnées célestes. Il s’ensuit qu’on s’accorde à diriger cette part selon les deux mouvements, comme une planète: dans le sens de la succession des signes zodiacaux, et dans le sens du mouvement diurne. 

En revanche la part horaire est un cercle, comme l’horizon. Elle n’a pas de coordonnées célestes, mais seulement une distance horaire et un degré de passage. Ce dernier correspond au point où l’écliptique coupe le cercle, tout comme l’horoscope est le point où l’écliptique coupe l’horizon. Il s’ensuit que la direction de la part lunaire adviendra exactement comme la direction de l’horoscope c'est-à-dire uniquement dans le sens zodiacal et non pas dans le sens opposé: tout comme les degrés des directions «dans le zodiaque» montent à l’horoscope selon les ascensions obliques ou descendent à l’Occident selon leurs descensions, les degrés eux-mêmes monteront, ou descendront, vers le cercle de la part selon les ascensions, ou descensions, obliques de ce cercle. Aucune autre direction de la part horaire ne peut être tolérée.

figure 5

Cette image animée est tirée de la 6e leçon du Cours «Fondements astronomiques et notions élémentaires d’astrologie classique» de Giuseppe Bezza et Marco Fumagalli.

1) () la part de Placide Elle repose sur la distance équatoriale entre la Lune (AR) et le degré d’équateur qui se lève avec le Soleil (AO), calculée sur le parallèle de déclinaison de la Lune. Elle se meut dans le monde seulement en vertu du déplacement de la Lune en ascension droite par rapport au Soleil durant le jour. Sa position indique toujours le lieu où se trouverait la Lune si, les positions des luminaires étant arrêtées, nous faisions pivoter la sphère en avant ou en arrière jusqu’à ce que le Soleil se lève. Elle indique donc toujours la phase lunaire telle qu’elle apparaît au lever du Soleil.

2) () la part «horaire» de Brunacci Elle repose sur la distance progressive entre la Lune et le Soleil, calculée dans le monde (distance horaire). Elle coïncide exactement avec la part de Placide au lever du Soleil. Elle se meut dans le monde seulement en vertu des distances horaires diverses prises par les luminaires au cours de la rotation de la sphère. Sa position indique toujours le lieu où se trouve l’horoscope lunaire, c'est-à-dire le cercle iso-horaire qui a vis-à-vis de la Lune la même distance que l’horoscope vis-à-vis du Soleil.

3) () la part «vulgaire» Elle repose sur la distance progressive entre la Lune et le Soleil prise en longitude. Elle pourrait coïncider avec les deux parts précédentes seulement au lever du Soleil si la Lune était dans l’un de ses Nœuds (latitude 0°). Elle se meut dans le monde en vertu de deux facteurs: le déplacement en longitude de la Lune par rapport au Soleil et surtout l’inclinaison différente de l’écliptique durant le jour, qui change la position horaire du degré de la part. Sa position sur l’écliptique, observée par rapport au degré qui se lève, indique la phase lunaire. Sa position dans le monde n’indique rien.