Una nuova formula per i poli.

(Phôs 1, dicembre 2000)

 
  Quando troviamo l’ascensione obliqua di un astro nel suo circolo orario (aoch), ovvero nel suo polo, questo significa che, se ci spostiamo alla latitudine geografica corrispondente a questo polo e facciamo sorgere l’astro, deve sorgere all’orizzonte il grado esatto di equatore che corrisponde all’aoch che abbiamo trovato. Per questo motivo, nelle direzioni e nella domificazione, possiamo usare le tavole di ascensione obliqua, redatte per le latitudini geografiche, entrando con il dato dell’astro come se stesse sorgendo a quel dato orizzonte. Tuttavia, applicando le formule consuete per il calcolo dei poli, questa corrispondenza non è perfetta. O meglio, talora lo è con un’approssimazione accettabile, talora no. Naturalmente, lo stesso problema vale per le discensioni oblique dalla parte opposta dell’orizzonte. 

Il metodo precedente.

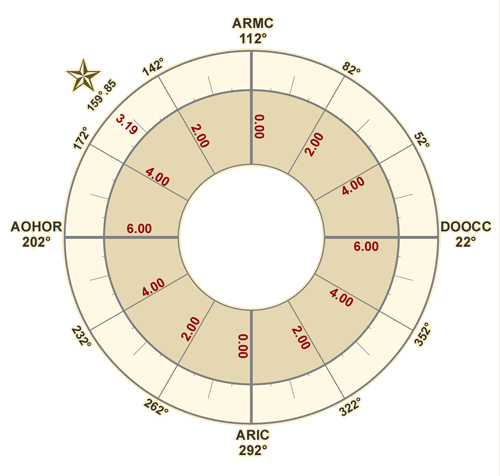
  Facciamo un esempio: al polo +30° culmini il grado 112° di equatore (armc) e un astro sia posto a 174°,09 di ascensione retta e a +38° di declinazione. La differenza ascensionale (da) è 26°,81, le ore temporali diurne (htd)19°,47, la distanza retta (dr) 62°,09 e dunque l’astro si trova ad una distanza oraria (dh) di 3,19 ore dal mediocielo, in XI casa. Calcoliamo ora la sua ascensione obliqua nel circolo orario:

  Ora troviamo l’elevazione del polo sul circolo orario, ovvero il polo dell’astro () con la formula consueta, quella che usiamo anche per i poli delle case:

dove damax sta per massima differenza ascensionale dell’eclittica al polo del luogo , ed sta per l’obliquità dell’eclittica che assumeremo con il suo valore medio di 23°27’. Troviamo subito la damax con la formula per la differenza ascensionale, dove la declinazione è quella massima dell’eclittica ( = ):

  Procediamo ora con la formula del polo:

  Ora dovremmo aspettarci che, alla latitudine geografica +17°,19, l’ascensione obliqua del nostro astro sia esattamente 159°,85. Calcoliamo la sua nuova differenza ascensionale che chiameremo dach poiché siamo al polo dell’astro:

e dunque avremo

Siamo piuttosto distanti dal risultato che ci aspettavamo.

Il nuovo metodo.

  Dopo alcune prove di calcolo nei pomeriggi piovosi della scorsa estate, notai che questa piccola differenza variava con il variare della declinazione: aumentava se la declinazione si discostava maggiormente da 23°27’ mentre diminuiva nel caso contrario. Ne ricavai la conclusione che la formula dei poli andava sostituita con una diversa, che tenesse conto dell’effettiva declinazione dell’astro ed anche della sua differenza ascensionale (da): Ovvero: andava sostituita con e damax con da!

Proviamo ora a rifare il calcolo del nostro esempio:

Spostiamoci ora a questo polo e calcoliamo la nuova differenza ascensionale e l’ascensione obliqua:

e dunque avremo

  Ora ci siamo! La piccolissima differenza è dovuta solo agli arrotondamenti dei decimali e scompare completamente se conserviamo tutti i decimali nel calcolo.

Conclusione.

  Questa nuova formula, più semplice e immediata della precedente, è in realtà l’unica formula corretta per calcolare i poli, mentre quella precedente (che usa damax ed ) ne è un adattamento necessario per il calcolo delle cuspidi nella domificazione placidiana. Infatti, se ancora non conosciamo le coordinate celesti del punto che cerchiamo (la cuspide), non possiamo conoscerne la differenza ascensionale (poiché la declinazione è ignota) e dunque dobbiamo cercarne il polo adattando la formula ad una situazione estrema: la differenza ascensionale non potrà essere superiore a quella dell’eclittica in quel luogo (da diviene damax) e la declinazione non potrà essere superiore a quella dell’eclittica ( diviene ). Ecco che allora troveremo i poli delle cuspidi di Placido con una approssimazione tanto migliore quanto più la cuspide si troverà vicina ai solstizi ( ± 23°27).

  Ho poi trovato questa identica formula in Robert De Luce, Complete Method of Prediction, New York 1935, p. 38, che riporta: “ log sine Q plus log cot. decl. = log tan pole ”, dove Q rappresenta la dach, ovvero la differenza ascensionale al polo dell’astro.