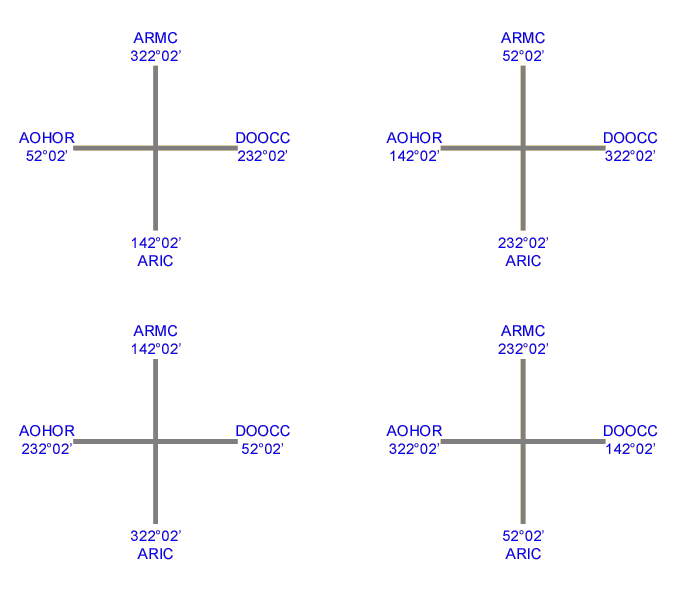
Mi sembra utile illustrare con un esempio il principio esposto da Ibn 'Ezra. Sia una nativita a Vienne (Rhône) latitudine 45°; 30, longitudine 4°; 49 E, il 21 Gennaio 1975, 13h 8m a.m. H.G. e determiniamo le cuspidi delle dodici case secondo il metodo del Titi e del Diedo.

  Premesso che ogni punto dell'eclittica si porta avanti il proprio arco diurno, per conoscere il semiarco diurno (SAD) di ogni grado devo moltiplicare per 6 le ore temporali diurne di quel grado. Ibn 'Ezra pone pertanto innanzitutto due relazioni che vogliono significare che la differenza ascensionale (DA) di un semiarco viene consumata se positiva ed eccedente l'angolo retto, acquistata se negativa e minore dell'angolo retto. Ciò avviene dal sorgere al culmine, dal culmine al tramonto. Questo rapporto sussiste in virtù della proprietà tra la linea meridiana e la linea dell'orizzonte, le quali, intersecandosi, formano sempre quattro angoli retti. Sorgendo, culminando o tramontando 52°; 02 tempi del cerchio equinoziale, sorgeranno, culmineranno e tramonteranno sempre luoghi del cerchio equinoziale separati da un angolo retto o da un multiplo di angolo retto, vedi fig. 2.

  Ibn 'Ezra risolve elegantemente la questione della differenza ascensionale affermando, da un lato, che la differenza in tempi di A.R. tra l'angolo del Medio cielo e l'angolo d'oriente è pari a sei ore temporali diurne del grado d'oriente; d'altro canto, la differenza in tempi di A.O. fra questi due angoli è pari a sei ore temporali diurne del grado culminante:

  Dopo questa premessa, segue un analogo ragionamento relativo all'inizio di ogni casa, la cui dimostrazione fo seguire per punti:

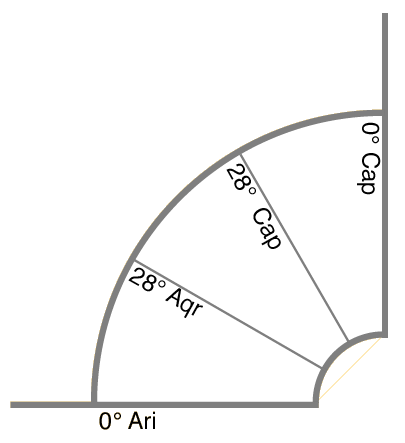
  Ibn 'Ezra prosegue quindi dichiarando il principio astronomico di questa ripartizione delle dodici case. Questo fondamento altro non è che il prodursi di una configurazione tra un corpo celeste ed un angolo in virtù del moto perpetuo della sfera e secondo il passo orario di quel corpo celeste. Questo principio ci appare pertanto apertamente "placidiano"; in quanto al Diedo, su questo punto non pare essersi chiaramente espresso.

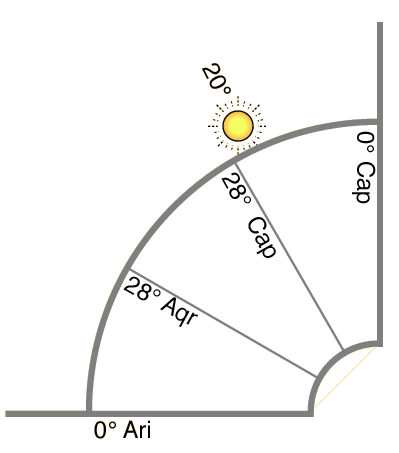
  Ibn 'Ezra dichiara in seguito di avere esposto il principio della ripartizione delle dodici case, in modo facile a intendersi, nel suo trattato sull'astrolabio.[8] Ma la nostra curiosità ci spinge a chiederci quale principio avessero in mente il biasimato al-Khwârizmî e il suo commentatore; in virtù di quale moto o cerchio o proporzione pongono 28° Capricorno alla cuspide dell'XII casa. Assumendo la terza parte del semiarco diurno del grado dell'oriente (ovvero la doppia ora temporale dell'oroscopo), essi l'aggiungono all'A.R. MC. e ne proviene l'A.R. XI; sommando quindi quattro HTd. HOR all' A.R. MC. proviene l'A.R. XII e così di seguito lungo tutto il semicircolo ascendente.

  Questo modo del ripartire le case aveva i suoi partigiani, come è giusto ed il suo propugnatore in Occidente apparve, capricci della fama, l'Alcabizio. Ci si ricordi dell'avversario di don Ferrante, quel «dotto attaccato ferocemente alla domificazione dell'Alcabizzo». Ma quale il principio? Non sappiamo. Ripetiamo le parole del Titi: «Altri determinano le cuspidi delle case mediante doppie ore temporali assunte nello zodiaco, in modo tale che il grado zodiacale che dista dall'orizzonte due ore temporali si trovi alla (cuspide della) dodicesima casa, quello che ne dista quattro alla (cuspide della) undicesima, ecc. In seguito da questi punti descrivono circoli di posizione che passano per i punti di intersezione dell'orizzonte e del meridiano. Quale sia poi il fondamento di questi circoli di posizione, confesso di non comprendere»[9].

  In altri termini, secondo questa divisione, la distanza in tempi di ascensione retta tra la XII e l'oriente sarà di due ore temporali del grado dell'oriente, tra l'XI e l'oriente di quattro ore temporali del grado dell'oriente. Nell'esempio portato da Ibn 'Ezra:

  Una tale divisione non tiene in alcun conto la differenza ascensionale del semiarco diurno dell'oriente, sclerotizza il semiarco e lo snatura. E' una ripartizione viziata e imperfetta: infatti, fondandosi sul semiarco, ne trascura il fondamento, che è il moto. Affinché la ripartizione delle case «sia naturale - afferma nel luogo citato il Titi - deve essere compiuta mediante parti fra loro proporzionali». Questa proporzionalità è chiaramente espressa da Ibn 'Ezra ove dichiara che l'afeta, posto all'inizio dell'XI casa, deve necessariamente distare due ore temporali del suo grado dal culmine. Questa proporzione è ancora evidente quando si afferma - secondo l'opinione di tutti quanti gli astrologi - che tra l'angolo culminante e l'angolo che sorge vi sono sei ore temporali del grado dell'oriente. Ma questa proporzione non è più mantenuta nella ripartizione delle rimanenti cuspidi secondo la domificazione attribuita all'Alcabizio.[10]

  La divisione delle case che porta il nome dell'Alcabizio fu ritenuta in Occidente «Arabum opinio, et antiqua»,[11] «modus primus et usitatissimus».[12] Antica, giacché appare espressa nel sec. V da Rhetorio;[13] degli Arabi, in quanto la si trova esposta da al-Battani e da altri,[14] sicché era opinione di alcuni che questa stessa concezione fosse quella di Ibn 'Ezra.[15] E' ora doveroso citare la conclusione dell'esposizione di Ibn 'Ezra, ove l'astronomo ebreo espone il modo di reperire le cuspidi:

  In altri termini: la cuspide dell'XI casa (cfr. esempio di Ibn 'Ezra), posta a 20° Capricorno, risponde al vero, in quanto la differenza in A.R. tra XI e X è pari a 2 HTd. XI. Ma se, in assenza di ogni tavola all'uopo predisposta, devo cercare una cuspide, ovvero un luogo che sia lontano dal meridiano due o quattro ore temporali secondo il luogo che devo cercare, occorre procedere mediante successive approssimazioni. Es.: A.R. MC. 270 + 1/3 delle A.R. del quadrante (30) = 300, A.R. di 28° Capricorno, le cui Htd, moltiplicate per due, danno 22.20.02; giacché 22.20.02 < 30, ne consegue che il grado che cerco è minore di 28° Capricorno. Dovrò pertanto diminuire, finché troverò un grado le cui ore temporali duplicate producono la sua distanza retta dal MC.[16]

  Procedimento troppo complesso? Forse, ma non dimentichiamo che è possibile materializzare una rete di linee orarie su un planisfero, come testimoniano Ibn 'Ezra stesso ed Enrico Bates.[17] D'altro canto si è soliti prestare agli antichi astrologi, come pure a quelli a noi lontani, il "dono della semplicità" o, per così dire, un abito di vita semplice che ben si accompagna ai grandi intelletti. Questa attitudine è caratteristica negli astrologi del Cinquecento. Afferma Valentino Nabod: non possiamo negare che la divisione delle case di 30 in 30 gradi misurati sul cerchio dell'eclittica (l'inqualificabile modus aequalis) sia quella di Firmico, di Albohali, di Albumasar, di Albubater e di Guido Bonati.[18] Ma come possiamo affermarlo? In virtù della simplicitas degli antichi? ma una tale semplicità denoterebbe piuttosto uno scarso intelletto o almeno poca esperienza e, in verità, questa divisione delle case lungo l'eclittica fu escogitata per la prima volta da Giovanni Schöner e dal giovane Cardano, quale presunto, antico sistema degli antichi.[19]

  Questo procedimento è esclusivo di Ibn 'Ezra? E se lo è, perché l'astronomo ebreo indirizza in particolare la sua critica ad al-Khwârizmî, espositore del sistema da noi conosciuto come "domificazione dell'Alcabizio", allorché tale sistema sembra essere ripetuto dalla maggior parte degli astronomi medioevali, arabi, ebrei o latini? Non è inverosimile supporre che la "domificazione dell'Alcabizio" e quella "di Ibn 'Ezra" siano in realtà la medesima: la sola differenza consisterebbe nella scomparsa, in quella dell'Alcabizio, delle approssimazioni successive. Ma tale scomparsa implicherebbe altresì la dimenticanza di un principio astrologico che è fondamento delle familiarità degli astri: la distanza proporzionale da cuspide a cuspide in virtù delle ore temporali successive.[20] In tal senso la critica che Ibn 'Ezra rivolge ai compilatori di tavole astronomiche, quali ad es. Ha-Bargelonî,[21] mira a salvaguardare il principio dell'emissione di raggi tra gli astri in mundo, per usare una espressione del Titi, ovvero da casa a casa secondo quantità degli archi diurni o notturni degli astri.

  L'esatta ripartizione delle case non è quindi un problema marginale, non è una questione di lana caprina, non riposa su un principio simbolico, ma rigorosamente astronomico.[22] Chiunque, prima di giungere ad un diverso partito, voglia considerare (ma se non vuole, io qui l'avverto) che gli aspetti tra gli astri sono di due generi fondamentali: l'uno nello zodiaco, l'altro secondo il loro procedere orario, e che non v'è giudizio ove ciò si possa tralasciare, sotto pena di abdicare al giudizio stesso o di affermare il falso.

1. Ephemerides exactissime caelestium motuum ad longitudinem Almae Urbis et Tychonis Brahe Hypotheses...ab anno 1641 ad annum 1700, Lugduni 1677, I, 368; cfr. I, 498: «Caeterum si libuerit hoc ordine construere figuram secundum ordinem ptolemaicum sumendi sunt numeri polares ptolemaici».

2. H. Selva, La domification ou construction du thème céleste en astrologie, Paris 1917, p. 32. Ma cfr. P. Choisnard, Langage Astral, Paris3 1983, 71.

3. Abraham Ibn 'Ezra, Le livre des fondements astrologiques, tr. J. Halbronn, Paris 1977, 295s.; mi astengo dal citare il testo, che ha subìto un evidente disordine.

4. El libro de los fundamentos de las Tablas astronómicas de R. Abraham Ibn 'Ezra, edición crítica, con introducción y notas por José M.a Millas Vallicrosa, Madrid-Barcelona 1947, 159-160.

5. Propongo di leggere così il testo anziché: «ad principium 3e horarum, 4 temporales in tabula circuli recti».

6. Doronius = Doroteo di Sidone; Meschela = Mâshâ'allâh; anche al-Zarqalî sembra dividere le case secondo il principio di Ermete, cfr. Millas Vallicrosa, Estudios sobre Azarquiel, Madrid-Granada 1943-1950, p. 47.

7. al-Khwârizmî e il suo commentatore Ibn al Mutannâ', di cui vedasi E. Millas Vendrell, El Commentario de Ibn al-Mutanna' a las Tablas Astronomicas de al-Jwârizmî, Madrid-Barcelona 1963, pp. 149-150.

8. Su questo trattato cfr. quanto afferma Ibn 'Ezra, Abraham Iudei de Nativitatibus... Venetiis 1485, fo. 3r; cfr. J.M. Millas Vallicrosa, Un nuevo tratado de R. Abraham Ibn 'Ezra, Al-Andalus n. 5, 1940, pp. 1-29; Idem, Sobre un 'Tratado de astrolabio' atribuido a R. Abraham Ibn 'Ezra, Sefarad n. 4, 1944, pp. 31-38. Sulle opere di Ibn 'Ezra tradotte in latino cfr. L. Thorndike, The latin Translations of the Astrological Tracts of Abraham Avenezra, Isis n. 35, 1944; R. Levy, Note on the Latin Translators of Ibn 'Ezra, Isis n. 37, 1947. Un simile astrolabio fu costruito e descritto nei suoi dettagli da Enrico Bates di Malines, su richiesta di Guglielmo di Moerbeke, cfr. Magistralis compositio astrolabij Hanrici Bate..., in: Abraham Iudei de nativitatibus, cit., fo. 22b: «Sed quia iudiciorum auctores aliqui equationes aspectum ed directionum super horas temporales et earum partes, sicut et domorum equationes prout in eorum apparet operibus fundaverunt, idcirco ut hic modus instrumento ultro se nobis offerret hanc divisionem ingeniatus fui...»

9. Physiomathematica sive Coelestis Philosophia, Mediolani 1675, p. 174.

10. Se aggiungiamo sei ore temporali del grado che sorge all'AR.MC, otteniamo l'AR.MC quando il grado dell'oriente transita al meridiano, avendo consumato tutto il suo semiarco diurno. Allo stesso modo possiamo porre le seguenti relazioni per le cuspidi intermedie:
AR.MC + 2HTd.HOR = AR.MC quando il grado dell'oriente sale alla XII
AR.MC + 4HTd.HOR = AR.MC quando il grado dell'oriente sale all'XI

11. G. Cardano, Commentariorum in Ptolemaeum de Astrorum iudiciis libri IV, Opera Omnia V, Lugduni 1663, p. 167.

12. Clarissimi doctoris Joannis de Monteregio Germani Tabulae directionum... per...Lucam Gauricum..., Venetiis 1524, fo. 7r.

13. Catalogus Codicum Astrologorum Graecorum VIII/I, pp. 221-223.

14. Al Battani, Opus Astronomicum, ed C.A. Nallino, il quale nota (I, p. 248) come la ripartizione delle case di al-Battani si ritrovi in molti astronomi arabi e, nei Libros del saber de Astronomia (ed. M. Rico y Sinobas) II, p. 193, tale ripartizione è ascritta, oltre che a Tolomeo, a Vettio Valente (Veles). Ma su ciò occorrerà ritornare.

15. V. Nabod, Enarratio elementorum astrologiae..., Coloniae 1560, p. 116; non così Giovanni di Sassonia, che presta a Ibn 'Ezra diversa opinione, ma, poiché «ista via communiter non tenetur, ideo non curo eam multum explanare», Libellus isagogicus Abdilazi, idest servi gloriosi dei, qui dicitur Alchabitius ad magisterium iudiciorum astrorum interpretatus a Joanne Hispalensi, scriptumque in eundem a Joanne Saxonie editum, Venetiis 1512, fo. 39r.

16. Un esempio di procedimento in assenza di tavole appositamente predisposte, senza l'uso della trigonometria sferica, con il solo ausilio di una tavola di A.R. e di ore temporali, lo si può trovare in Fomalhaut (Charles Nicoullaud), Manuel d'astrologie sphérique et judiciaire, Paris2 1933, 76s.

17. «Potremo trovare ancora i cuspidi secondo il corso dell'ore assai giusti, con farci un planisfero ad imitazione di quello già fatto intorno all'orologio del tempio d'Argentina dallo spirito egregio del valoroso Curando Dasipodio (Cunradus Rauchfuss), matematico raro, et illustre; e come già quel non mai appieno laudato intelletto del chiarissimo Livio Sanuto nostro venetiano...» G. Diedo, L'anatomia celeste, Venetia 1593, fo. 8r.

18. V. Nabod, op. cit., 118.

19. Io. Schonerus, De iudiciis nativitatum libri tres, Norimbergae 1545, fo. 148v-152r; ripreso in Tabula resolutae astronomicae, Witenbergae 1587.

20. Cfr. in H. Bate, op.cit., il capitolo: De aspectibus planetarum inveniendis secundum mentem Ptholomei et Albumaçar et aliorum quam plurium : «Apud artis astrologice periciores unanimis est concordia: quod planeta in exordio domus cuiuslibet constitutus principium domus tertie succedentis in serie domorum et domum undecime antecedentis initium: aspectum sextili aspicit..»

21. La obra Séfer Hesbón mahlekot ha-kokabim de R. Abraham bar Hiyya ha-Bargelonî, ed. critica, trad., intr. y notas por José M.a Millás Vallicrosa, Barcelona 1959, pp. 96-98.

22. Una chiara esposizione della domificazione dell'Alcabizio si trova in A. Bausani, Appunti di astronomia e astrologia arabo-islamiche (Università degli studi di Venezia), Venezia 1977, pp. 170-179.