Placido Titi, Coelestis Philosophia 2,3

Quali sono i generi di familiarità degli astri.

traduzione di Giuseppe Bezza (Schema 1, 1986)


  Non mancano astrologi (mathematicarum rerum Professores) che assumono i raggi non solo lungo il circolo dei segni, ma anche su altri circoli: vuoi secondo l'ascensione retta dei luoghi, vuoi secondo le ascensioni oblique, vuoi secondo le ascensioni miste e ancora in altri diversi modi; si vedano ad esempio Magini, Giovanni di Sassonia e altri.
  Da parte mia, considerando le familiarità delle stelle in funzione del loro moto reale e del loro influsso (1), ritengo che non vi siano altri raggi al di fuori degli influssi proporzionali che provengono da proporzionali distanze acquisite in virtù del moto e a partire dai termini del moto medesimo; e mediante le quali distanze influiscono determinati e proporzionali gradi di intensità delle qualità loro. Pertanto ammetto tanti generi di raggi quanti sono i moti degli astri, mediante i quali influiscono successivamente e producono determinate distanze; per questa e non per altra ragione compiono e manifestano determinate qualità nel moto successivo.
  Noi percepiamo con i nostri sensi come il moto delle stelle sia duplice: l'uno nella concavità del primum mobile (2) dalle regioni occidentali a quelle orientali; l'altro unitamente al primum mobile dall'oriente all'occidente.
  Avviene in effetti che, in entrambi i moti, gli astri producono quattro passiones luminis (3), mediante le quali suscitano, in virtù del loro influsso, le quattro qualità prime nelle cose inferiori. Ritengo pertanto che due siano i principali generi di familiarità riconoscibili: l'uno nel circolo dei segni sotto il primum mobile , l'altro nel mondo secondo le distanze da casa a casa.

  Prima conclusio: le mutue distanze proporzionali tra gli astri nello zodiaco sono familiarità vere ed efficaci, come Tolomeo tramanda ex professo ed è in ciò seguito da tutti gli astrologi. Questa conclusione può essere dimostrata ottimamente e da quanto è stato detto e da quanto dovrà ancora dirsi.

  Secunda conclusio: queste familiarità assunte nello zodiaco sono vere ed efficaci unicamente fra stella e stella, le quali sono entro lo zodiaco e si muovono di moto proprio, non sono vere rispetto ai cardini e alle case.

  Explicatur: affermo che gli astri, allorché si trovano tra loro in distanze proporzionali assunte lungo lo zodiaco, si osservano mutuamente con raggi veri ed efficaci. Al contrario, se il luogo della distanza proporzionale - o se vogliamo del raggio di una data stella - assunto nello zodiaco ascenda a un dato cardine o casa, ritengo che tale raggio non è vero né efficace, ma inane e privo di effetto. Pertanto le familiarità degli astri ai cardini e alle case assunte nello zodiaco non sono vere ed efficaci, né sono raggi attivi, ma sono posti ed assunti a puro arbitrio umano e non secondo natura. Nessuno prima d'ora ha affermato questo principio (4).

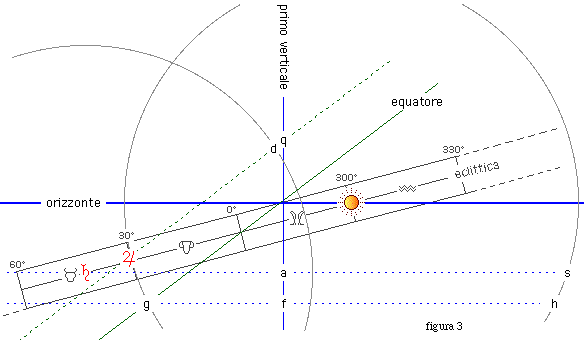
Nella fig. 3 ad es. il Sole è all'oroscopo e Giove ha un sestile al Sole: dico che il sestile di Giove all'oroscopo non è efficace, dico che non è neppure un raggio, ma una distanza inane e inefficace. Allo stesso modo nella fig. 4, posto Giove a gradi zero di Pesci o di Scorpione, non è in trigono all'oriente, né in sestile, pur se sorgessero gradi zero del Cancro o del Capricorno.

  Probatur primo: i raggi delle stelle rispetto ad un soggetto determinato devono essere parti proporzionali di un influsso reale, che gli astri portano a compimento allorchè mutano, in virtù del moto, la distanza rispetto a quel soggetto medesimo. Tuttavia i raggi degli astri ai cardini e alle case non sono assunti nello zodiaco, ergo etc. La proposizione maggiore è manifesta dagli argomenti del primo libro, la minore viene così dimostrata: gli astri non portano a compimento il loro influsso rispetto ai cardini e alle case lungo lo zodiaco, in quanto lo zodiaco non è la via delle stelle ai cardini; gli astri infatti quando passano da un cardine ad un altro non progrediscono lungo lo zodiaco, pur se sono in esso presenti; se d'altro canto progredissero lungo lo zodiaco si muoverebbero contro l'ordine dei segni; al contrario le stelle vanno ai cardini unitamente ai gradi dello zodiaco in cui sono reperite (non diversamente che se i pianeti fossero stazionari e quindi non mutano luogo nello zodiaco transitando da un cardine all'altro). Ergo i raggi delle stelle ai cardini e alle case, assunti nello zodiaco, non sono parti reali del loro influsso rispetto ai cardini e alle case medesime. Nella figura 3, ad esempio, Giove, posto a gradi 0 del Toro, non va all'oroscopo muovendosi sullo zodiaco (in tal modo progredirebbe contro l'ordine dei segni, ovvero da gradi 30 dell'Ariete a 29, 28, 27 etc., ciò che è assurdo); la via di Giove all'oroscopo è per contro la linea Giove-d-q , parallela all'equatore, e nessun'altra.

  Secundo: quando una stella è al meridiano osserva sempre entrambi gli angoli dell'orizzonte con un raggio quadrato; tuttavia lungo lo zodiaco assai raramente si produce un raggio quadrato dal meridiano all'orizzonte (ovvero solo nei punti tropici), ergo i raggi ai cardini computati nel circolo dei segni sono inani. La proposizione minore è manifesta, la seconda si dimostra: primo in Tolomeo, cap. de locis apheticis : "il luogo che è in quadratura alla linea dell'oriente, ovvero quello che culmina sull'orizzonte". E se tu dicessi che Tolomeo intende parlare dei raggi nell'equatore, la mia argomentazione sarebbe comunque soddisfatta, giacchè ne conseguirebbe che, secondo la dottrina di Tolomeo, non è qui questione di raggi nello zodiaco. Secundo : quando una stella è al meridiano, si trova a una distanza intermedia fra l'oriente e l'occidente, ovvero dalla congiunzione con l'oriente alla sua opposizione diametrale; ora, la distanza intermedia tra la congiunzione e l'opposizione è il raggio quadrato, come è d'altronde manifesto e come insegna Tolomeo, cap. de XII locorum configurationibus (1,12): "in seguito, se prendiamo le due frazioni e i due superparticolari principali nella musica e se applichiamo le frazioni 1/2 e 1/3 al diametro, che è costituito di due angoli retti, l'uno produrrà la figura del quadrato...". E' qui evidente che Tolomeo intende che la metà della porzione massima, compresa tra la congiunzione e l'opposizione, costituisce il quadrato. Tuttavia, nel nostro esempio, la porzione massima che deve essere divisa in due parti uguali non può trovarsi nello zodiaco. Essa non può altrimenti essere compresa che tra la congiunzione e l'opposizione della stella, ovvero dal suo sorgere al suo tramontare. Ciò non può operarsi nel circolo dei segni, ergo etc.
  Si veda ad es. la figura 4: Giove è al meridiano ed osserva entrambi gli angoli dell'orizzonte, l'oriente e l'occidente, con raggio quadrato, in quanto si trova ad una distanza intermedia tra il sorgere e il tramontare, intendo dei suoi punti medesimi del suo sorgere e del suo tramonto, che sono a e b. Ora se i punti in cui Giove sorge e tramonta distassero dalla linea dell'eclittica, nulla importerebbe alla questione presente. Nel nostro caso infatti, la porzione massima deve essere divisa in raggi, ma il circolo del moto di Giove, del suo influsso, intendo la linea che l'astro descrive dal sorgere al tramonto suoi: a-Giove-b, ovvero il circolo che passa tra il punto del sorgere di Giove fino al punto del suo tramontare, attraverso la linea del suo moto diurno.

  Tertio: se fossero veri i raggi delle stelle ai cardini assunti nel circolo dei segni, sarebbe necessario che la stella, al suo tramonto, sia distante dall'oriente 180 gradi, tanti infatti sono i gradi dello zodiaco che esprimono l'opposizione. E' tuttavia falso affermare che una stella, allorché tramonta, disti sempre 180 gradi dall'oriente. Infatti una stella che non sia sita sull'equatore, se ha declinazione boreale, dista più di 180 gradi allorchè tramonta; se ha declinazione australe, meno. In verità si dice che un mobile dista di tante parti dal punto iniziale del suo moto quante ne ha percorse ed illuminate nel suo cammino, non più, non meno. Sarebbe d'altro canto falso affermare che chi si allontana da Roma, avendo percorso cinque miglia, ne sia distante dieci; e se distasse dieci miglia considerando una diversa strada, è nondimeno sciocco calcolarne la distanza su una via diversa da quella lungo la quale procede. Ad es., una stella posta sul circolo tropico invernale, alla elevazione polare di gradi 43, avrà percorso al momento del suo tramonto dall'oriente all'occidente 132 gradi e non si può quindi affermare che dista 180 gradi, se ancora non li ha compiuti nel suo percorso. Posta sul circolo estivo, la stella avrà invece percorso 228 gradi. Ora, per quale ragione si può mai affermare che dista 180 gradi se ne ha percorsi molti di più? nessuna di certo (5).

  Dices: lo sguardo (intuitus) altro non è che una data distanza proporzionale, ma non vi è che una sola proporzione, quella che si produce lungo lo zodiaco, al di fuori del quale non vi è proporzione alcuna. Tolomeo (cap. de XII locorum configurationibus) considera soltanto le configurazioni nello zodiaco e nel medesimo capitolo espone che la ragione delle figure convenienti è la consimilitudine dei segni, così come di quelle inconvenienti è la dissimilitudine. Pertanto la natura delle figure non dipende né può dipendere che in minima parte da ragioni che non siano la natura stessa dei segni, giacché al di fuori dei segni le figure non hanno alcuna natura, né qualità attiva.

  Respondeo: primo negando la proposizione minore. Il passo citato di Tolomeo, se interpretato in tale senso, si opporrebbe a quanto egli stesso insegna cap. de locis apheticis (3,11), ove attribuisce configurazioni anche alle case del cielo, sebbene non sia in esse contenuta la natura dei segni. Si opporrebbe inoltre a quanto afferma cap. quae nam sunt vitae moderandae rationes , ove giudica che anche le configurazioni convenienti tra i segni, il trigono ed il sestile, si deformano mutandosi in figure letali in virtù della breve o lunga ascensione loro. Respondeo secundo : poiché i raggi sono determinate distanze proporzionali, possono essere - e sono naturalmente - tanti quanti sono i modi con i quali gli astri creano ed aumentano le distanze. Invero gli astri compiono una duplice distanza, una fra di loro lungo lo zodiaco, e di questa parla Tolomeo nel luogo citato (1,12), ove tratta apertamente delle configurazioni tra i segni; l'altra rispetto ai cardini. In questa seconda forma gli astri producono distanze descrivendo linee parallele all'equatore; in effetti, come è già stato detto, gli astri non producono una distanza rispetto ai cardini, né l'aumentano, procedendo lungo lo zodiaco, ma lungo una linea parallela all'equatore. Ora, Tolomeo divide le dodici case del cielo in virtù di questo fondamento (vedasi cap. de locis apheticis e altrove); invero, nel definire le case, non assume quantità proporzionali del circolo dei segni: afferma infatti che la casa decima osserva sempre l'oriente con raggi quadrati e che essa coincide con il circolo meridiano che sempre, egli dichiara, giace sullo zenith, e che la casa undecima sempre osserva l'oriente con raggio esagonale, la nona osserva l'oriente con raggio trigonico, quantunque assai sovente accada che i segni, da queste case medesime, non osservino il grado del segno che si trova all'orizzonte o ancora, se l'osservano, l'osservano con diversi raggi.

  In seguito Tolomeo dichiara che la ragione della concordanza delle figure è la simiglianza di natura dei segni, tuttavia ad essa non attribuisce una ragione formale. Afferma infatti: "di queste configurazioni i trigoni e gli esagoni sono ritenute armoniose", sono ritenute dice, quasi volesse intendere che è un'opinione umana; allo stesso modo, poco oltre, riguardo ai raggi ostili: "sono reputate figure disarmoniche". In verità, come bene osserva il Magini seguendo il Cardano nel suo Primum Mobile, can.39 (6), il diametro si produce tra segni che concordano per sesso, nondimeno è più ostile del quadrato medesimo. Pertanto Tolomeo non attribuisce una ragione formale, né tanto meno sostiene che le configurazioni siano prive di valore al di fuori del circolo dei segni, come d'altro canto si può desumere da molti altri passi, ove chiaramente indica che anche nello spazio delle case si producono raggi proporzionali.

  Quarto probatur: Lo sguardo è una determinata distanza proporzionale ed una proporzione si assume in rapporto a date quantità, ovvero di quella che precede e di quella che segue. Ora, una quantità proporzionale non è materialmente diversa da una quantità non proporzionata, giacché, in quanto materia, consta di parti integranti. Ma la quantità precedente e seguente della distanza degli astri rispetto ai cardini non è misurabile sullo zodiaco o su una sua parte, come è stato dimostrato e come apparirà più chiaramente in seguito. Al contrario, essa è misurata dal moto e dall'influsso reale che gli astri, nel corso del loro irraggiamento, manifestano mentre procedono da un cardine all'altro. Pertanto questa proporzione quantitativa rispetto ai cardini non deve essere assunta nello zodiaco, ma nel moto stesso degli astri e nel loro influsso. E' così dimostrata la proposizione minore. La quantità della distanza è quella compresa dal termine in cui principia la distanza stessa e il moto al termine in cui giunge il corpo che si muove; invero qualsivoglia altro termine non conviene alla presente questione; d'altra parte si deve considerare che il termine in cui principia la distanza e il moto degli astri rispetto ai cardini non coincide con il luogo in cui sorgono i gradi dell'eclittica, ma con il luogo in cui è sorto l'astro medesimo. Vedasi ad es. la figura 4 ove sono descritte due medietà dello zodiaco: sia che sorgano gradi zero del Cancro o del Capricorno, Giove, che è sul meridiano a gradi zero dei Pesci (o dello Scorpione se si vuole), si trova in quadrato all'oroscopo; in effetti l'arco che esprime la sua distanza dall'oriente non è un arco dello zodiaco, ma un arco del parallelo che l'astro di Giove ha descritto nel suo percorso dall'oriente al meridiano.
  Ne consegue che i termini di ogni distanza delle stelle dall'orizzonte sono i loro propri punti del sorgere e del tramontare, non i punti in cui si levano e si coricano i gradi dell'eclittica.

  Tertia conclusio: i raggi degli astri ai cardini e alle case, calcolati secondo le distanze proporzionali ovvero secondo parti degli archi diurni e notturni delle stelle medesime sono familiarità vere ed efficaci, che io chiamo familiarità nel mondo (7).
  Per la comprensione di quanto precede occorre considerare che la distanza fra due punti può essere calcolata in modi sempre nuovi ed innumerevoli, in quanto si possono porre innumerevoli vie e linee sulle quali calcolare e misurare le distanze. In ciò consiste l'intera questione e dei raggi e dei circoli di posizione. Chi ad es. vuole misurare la distanza tra Roma e Venezia può farlo in tanti modi quanti sono le vie fra queste città, le quali vie sono pressoché infinite. Se invece non si debba calcolare la distanza fra due punti, ma fra un solo punto e una data linea, come ad es. tra il vertice di un triangolo e il lato della base, allora i modi con i quali possiamo calcolare la distanza dal vertice alla base sono tanti quanti sono i punti determinabili nel lato stesso della base, ovvero pressoché infiniti.
  Nel nostro caso vi è questione della distanza dal punto alla linea, ovvero della distanza della stella dalle linee delle cuspidi delle case, e la difficoltà è la seguente: si deve considerare la distanza della stella dal punto dell'eclittica iscritto nella cuspide della casa o dal punto per il quale è passato o passerà l'astro del quale si vuole misurare la distanza? Io affermo che occorre calcolare la distanza compresa tra il punto del passaggio dell'astro e l'astro medesimo e che questa distanza deve essere calcolata secondo quell'arco della sfera che rappresenta la via del moto dell'astro da un cardine all'altro.
  Questa conclusione è manifesta dagli argomenti precedenti. Dimostriamo nondimeno che i raggi altro non sono che le distanze proporzionali acquisite tramite il moto e l'influsso degli astri. Ora gli archi diurni e notturni delle stelle sono in verità i loro moti ed influssi medesimi rispetto all'orizzonte; quindi le parti proporzionali dell'arco diurno e notturno degli astri sono familiarità vere ed efficaci. La proposizione maggiore è palese da quanto dichiarato altrove; in effetti queste familiarità ai cardini e alle case, delle quali tratto, si misurano in virtù di una divisione proporzionale del reale moto di irraggiamento e di influsso degli astri e non già con il compasso, né con altra qualsivoglia divisione della quantità in quanto tale; siffatta divisione non sarebbe attiva.

  Dices: i raggi degli astri ai cardini considerati nello zodiaco sono parti reali del loro influsso e del moto loro, che essi compioni lungono il circolo dei segni e pertanto siffatti raggi non possono non essere naturali ed efficaci.

  Respondeo: l'influsso degli astri nel circolo dei segni è efficace rispetto ad altre stelle che sono site nel medesimo circolo e che ivi progrediscono. Invero, dopo la congiunzione corporale (coniunctio praesentialis) , protendono simultaneamente e proporzionatamente le qualità suscitate in tale congresso, mentre procedono successivamente lungo lo zodiaco, creando ed aumentando in esso le distanze fino al punto estremo delle loro mutue distanze proporzionali, dove nuovamente riproducono ogni irraggiamento ed influsso precedentemente mostrato in virtù del loro moto. Pertanto le mutue distanze proporzionali delle stelle lungo il circolo dei segni sono efficaci in virtù delle loro mutue separazioni ed applicazioni che compiono lungo il circolo zodiacale medesimo, ove appunto lanciano e rimandano le loro qualità in funzione delle distanze che compiono. Ora, in verità, i raggi sono distanze proporzionali che devono essere misurate e nel modo stesso in cui si compiono e rispetto ai termini in cui si producono e rispetto alla regione ove appare la loro percezione in virtù del moto, dell'irraggiamento, dell'influsso. Del resto, rispetto ai cardini e alle case gli astri non compiono le loro distanze muovendosi lungo il circolo dei segni: non procedono infatti lungo lo zodiaco nel loro avvicinarsi ai cardini e alle case, pur se nello zodiaco fossero siti, ma procedono tuttavia lungo lo zodiaco allorché permutano le loro mutue distanze, da stella a stella, in riferimento allo zodiaco medesimo.

  Dices: Tolomeo assume il diametro, quale figura dell'opposizione; ora il diametro deve passare per il centro del mondo, ma se assumessimo il diametro secondo il tuo modo, ovvero dal punto del sorgere dell'astro al punto del suo tramonto, siffatto diametro non passa per il centro del mondo, se non allorché la stella si trova sul circolo equinoziale; ne consegue che tale diametro non può essere assunto, etc.

  Respondeo: primo : Tolomeo stabilisce la figura dell'opposizione mediante il diametro in quanto tratta dei raggi assunti nel circolo massimo, lo zodiaco. Nel cap. de XII locorum configurationibus, infatti Tolomeo considera la divisione dello zodiaco e le configurazioni che in esso si costituiscono, onde manifestamente il diametro di un circolo massimo passa sempre per il centro del mondo. Tuttavia non è necessario che l'opposizione si produca sempre mediante il diametro per essere efficace e vera. Vi sono in effetti vere ed efficaci opposizioni, in base alle quali, prendendone noi la metà, costituiamo efficaci quadrati che constano di angoli retti (8). L'opposizione si produce pertanto anche in circoli minori, le cui linee diametrali non sono concentriche al mondo. Che anche in questi circoli - e non solo in quelli massimi - sia lecito assumere raggi e figure ne è testimone Naiboda apud Maginum de diebus criticis, quando afferma che i coluri sono separati da un quadrante sia presso i poli, sia all'equatore che è circolo massimo (9). E con ciò Tolomeo concorda, invero non vi sarebbe ragione per cui l'angolo del medio cielo (superior angulus) sia sempre in rapporto quadrato con l'oriente. Respondeo etiam che non è necessiario che il diametro dell'opposizione passi sempre per il centro del mondo: ogni stella, qualunque sia la sua latitudine e declinazione, allorché è all'occidente è in opposizione all'oriente e ad ogni stella che si trova all'oriente. La ragione è che tutta la regione dell'oriente fa opposizione alla regione dell'occiente, giacché di natura è di proprietà contrarie, in modo tale che qualsivoglia parte dell'oriente si oppone a qualsivoglia parte dell'occidente e viceversa (10).
  Ora, se la stella che sorge non ha la medesima quantità di declinazione della stella che tramonta e di segno contrario, non invia all'astro che si corica un diametro che passa per il centro del mondo, come è di per sè evidente; non è quindi necessario che il diametro dell'opposizione passi per il centro del mondo. E' manifesto che due stelle debbano dirsi opposte pur se hanno diversa declinazione allorché sono opposte in simile modo rispetto all'orizzonte della regione; in altro modo non può prodursi opposizione se non vi è uguaglianza nella quantità della latitudine.

  Dices: Tolomeo, cap. de his qui non nutriuntur (3,9) insegna che le opposizioni partili - quelle, intendo, il cui diametro passa per il centro del mondo - sono efficacissime; ne consegue che le rimanenti opposizioni sono sempre più deboli, in quanto distanti da tale diametro, e che pertanto solo le prime sono le vere opposizioni.

  Respondeo: Tolomeo assume in codesto capitolo le predette opposizioni per quanto concerne l'efficacia della malvagità degli astri infortunati, giacché occorrono diversi generi di raggi o, se vogliamo, di familiarità: si produca infatti un'opposizione nel primum mobile o circolo dei segni, si produca un'opposizione nel mondo e siano tutti paralleli; giacché infatti, come è stato detto e come verrà più ampiamente dimostrato in seguito, gli astri agiscono sia per raggi particolari, sia per raggi universali. Pertanto, affinché l'opposizione nello zodiaco sia efficace, è necessario che il suo diametro non si allontani dal centro del mondo; mentre, affinché sia efficace l'opposizione nel mondo, è necessario che il diametro non disti dalla superficie che si estende dal centro del mondo all'orizzonte e tale opposizione possiamo a buon diritto chiamare diametrale. Ecco ciò che è sufficiente al costituirsi dell'opposizione del mondo: non è necessario che il diametro passi per il centro del mondo, ma che sia condotto dal punto del sorgere al punto del tramonto dell'astro.

  Secundo probatur conclusio: i raggi mutui degli astri lungo il circolo dei segni sono veri ed efficaci per la sola ragione che, lungo il circolo medesimo dei segni, gli astri producono reciprocamente determinate distanze in virtù del moto loro suscitano ed estinguono le loro qualità muovendosi lungo linee parallele, pertanto i raggi delle selle ai cardini sono reali ed efficaci unicamente su tali linee parallele.

  Dices: non già per questa ragione, ma soprattutto perché l'eclittica è la via del Sole e il Sole è principio di ogni virtù dei viventi.

  Respondeo primo: se, in quanto via del Sole, l'eclittica deve avere la virtù di rendere reali ed efficaci i raggi degli astri misurati su di essa, ne consegue che un astro posto al di fuori dell'eclittica non recepisce i raggi di chi l'osserva. Se poi tu dicessi che un astro, pur lontano dall'eclittica, recepisce i raggi, e tuttavia più debolmente in quanto i gradi che sono lontani dalla via del Sole - causa efficiente della virtù di tale via - risultano più deboli quanto più distano dalla sfera di virtù dell'agente, respondeo che non è questo ciò che insegna Tolomeo quando richiede per l'efficacia dell'opposizione la simiglianza di diversa latitudine, per la congiunzione la medesima.

  Respondeo secundo: così come il Sole, descrivendo la linea dell'eclittica, le comunica tale virtù, che è la ragione maggiore, perché non potrebbe altresì comunicare una simigliante virtù ai paralleli che descrive perpetuamente in virtù del moto diurno? certo non vi è alcuna ragione contraria; e tuttavia non è questo il motivo maggiore, ma piuttosto in virtù del fatto che ivi gli astri compiono le loro distanze e perciò generano e alterano le qualità.

  Tertio probatur: i raggi devono essere assunti secondo la divisione proporzionale della quantità compresa fra i termini a quo e ad quem del moto degli astri. Ora la quantità del moto degli astri compresa fra questi termini altro non è che il loro arco diurno e notturno, ergo etc. La proposizione minore è pertanto manifesta: la quantità del moto degli astri ai cardini viene assunta dai punti, ovvero dai limiti degli istanti del sorgere e del tramonto degli astri medesimi, e da questi limiti si assumono gli archi diurni e notturni. E per quanto riguarda la dimostrazione della proposizione maggiore: la divisione di una data quantità non è proporzionale se non si compie in rapporto alla quantità precedente e seguente, dal termine a quo al termine ad quem della quantità medesima, come sovente è stato ripetuto. Ma la quantità del moto degli astri ai cardini non è la via dell'eclittica, non è il circolo dei segni, ma è un determinato parallelo. In verità, se si procedesse a una divisione dello zodiaco, tale divisione non potrà essere proporzionale, in quanto non proviene da un rapporto delle parti delle quantità del moto degli astri ai cardini. Ora, questo moto degli astri è l'arco diurno o notturno compreso fra il termine o punto a quo e il termine o punto ad quem del moto loro medesimo: questi termini sono i punti del loro sorgere e del loro tramonto. Ad es. nella figura 4 i punti del sorgere e del tramonto di Giove sono a e b, la quantità compresa fra questi due punti è l'arco diurno a-Giove-b e non l'arco di zodiaco 0° Cancro-Giove-0° Capricorno oppure 0° Capricorno-Giove-0° Cancro.

  Dices: i raggi ai cardini assunti nel circolo dei segni sono parti della quantità compresa fra gli astri e i cardini medesimi: quindi sono efficaci.

  Respondeo: in diversissimi modi, come ho più volte ripetuto, si può assumere la quantità o distanza di una stella dagli angoli, ma io affermo che fra tutte le diverse distanze sola è efficace quella compresa tra il termine a quo e il termine ad quem del moto degli astri; ed invero questa distanza di cui parlo non è una distanza zodiacale, ma una linea parallela all'equatore, descritta dalla stella nel suo giungere al cardine.

  Dices adhuc: l'arco dello zodiaco compreso tra il cardine e l'astro, è una quantità reale e definita fra due termini: intendo dalla linea del cardine e dall'astro.

  Respondeo: che per quanto attiene al secondo termine da te dichiarato, ovvero l'astro, non sussiste difficoltà alcuna. Al contrario, la linea del cardine è sì un termine reale che divide una parte della sfera e pertanto, in virtù di tale divisione, divide altresì il circolo dei segni, nondimeno lungo questa linea si possono assumere infiniti punti. Ora, di questi punti sono reali solo quelli determinati dagli astri medesimi allorché transitano per questa linea del cardine, punti ove gli astri costituiscono il secondo termine del moto. É questo che si deve pienamente comprendere.

  Quarta conclusio: i mutui raggi delle stelle, assunti secondo le distanze delle case, sono vere ed efficaci familiarità, che io chiamo mutue familiarità delle stelle nel mondo.

  Explicatur: sostengo che, se gli astri osservano con determinati raggi o distanze i cardini e le case, con medesimi raggi osservano parimenti le stelle che si trovano in quei cardini e in quelle case. Sia ad es. al culmine supremo una data stella, sia un'altra all'orizzonte: questi astri si osservano con raggio quadrato, giacché con raggio quadrato si osservano mutuamente i cardini in cui esse stelle son site; per quale ragione ciò si produca è detto nella conclusione precedente.

  Probatur primo: una stella all'oriente osserva con raggio quadrato la decima casa, pertanto gli astri che ivi fossero siti si osserveranno necessariamente con medesimo raggio quadrato. La premessa è manifesta, dimostriamo la conclusione: la casa è un circolo orario che si estende dal sud al nord; ora se gli astri osservano una data casa, osservano altresì tutte le stelle che in quella casa si trovano, qualunque sia la loro latitudine, qualunque sia la loro declinazione. Pertanto se una stella osserva dall'oriente la decima casa con raggio quadrato, osserverà altresì ogni stella ivi sita con il medesimo raggio quadrato. Nella quarta figura ad es. la stella g, posta all'oroscopo, osserva la decima casa con raggio quadrato, onde osserva anche quelle quattro stelle che si trovano nella decima casa, sicché a sua volta è da essa osservata con raggio quadrato.

  Secundo: ogni influsso delle case, ogni divisione del cielo dipende dalla luce e dall'influsso delle stelle. Invero, come verrà più oltre dichiarato nel cap. de domibus (11), se in cielo non fossero astri luminosi, non esisterebbero case, giacché non vi sarebbe irraggiamento e moto, dalle cui proporzionali parti le case assumono le proprie delimitazioni. Ne consegue per prima cosa una conclusione fondamentale: gli astri si osservano mutuamente dalle stesse case e pertanto osservano le case stesse. In effetti, se le stelle osservano le case secondo la distanza delle case, a maggior ragione si osserveranno l'un l'altra secondo il loro sito nelle case.

  Tertio: è comune opinione degli astrologi (Mathematicorum sententia), comprovata senza cessa dall'esperienza, che due stelle, pur se molto distino tra loro riguardo alla declinazione e siano nondimeno nel medesimo circolo (vuoi dell'orizzonte, o del meridiano o di un altro qualsivoglia circolo di posizione), siano tra loro congiunte (12). Ora una siffatta congiunzione si produce soltanto in ragione delle divisione in case (giacché invero due stelle non sono congiunte lungo il circolo dei segni se sono mutuamente distanti oltre la loro sfera di attività (sphaera activitatis) ovvero se le declinazioni loro distano più parti della estensione della loro virtù attiva) (13). Ne consegue pertanto che, se le stelle producono mutuamente una congiunzione in virtù della distanza delle case, occorre giudicare che esse compiono in virtù di questa medesima distanza delle case le rimanenti familiarità. Nella quarta figura ad es. le stelle site al meridiano sono congiunte fra loro per quanto attiene alla divisione delle case e al loro sito nel mondo. Ergo per queste medesime ragioni tutte e quattro le stelle predette sono in quadrato rispetto alla stella g.

  Quinta conclusio: i raggi assunti nell'equatore, secondo il modo proposto da Magini non sono familiarità reali ed efficaci (14).

  Explicatur: Magini, matematico fra i più celebri del nostro secolo, nel computare con assicurata precisione i moti, i circoli e le figure celesti, ritenne che, se le stelle proiettano i propri raggi in virtù di una data distanza lungo lo zodiaco, in virtù della medesima distanza devono proiettare gli stessi raggi in modo orbicolare. In tal modo il raggio quadrato appare un circolo massimo che divide la sfera in due parti uguali, mentre il sestile e trigono appaiono circoli paralleli e minori rispetto a detto circolo massimo, da esso parimenti distanti di 30 gradi. Ne consegue che, lungo questi circoli radiali gli astri intersecano, fra gli altri cerchi, anche il cerchio equatoriale. Sostiene pertanto il Magini che gli astri e i cardini recepiscono i raggi lungo l'equatore quando il luogo della sezione del raggio, collocato sulla linea equatoriale, giunge nel suo ascendere o nel suo discendere al luogo di posizione dei pianeti o ai cardini. Nella figura 3 ad es. dcs è appunto il circolo del raggio esagonale di Saturno e taglia l'equatore nel punto c ; ora, trovandosi questo punto all'oroscopo, in cui pure è il Sole, Saturno - secondo l'opinione del Magini - è in sestile al Sole nell'equatore. Dal canto mio ritengo inane tal raggio. Pur essendo ciò palese per le ragioni addotte nelle conclusioni precedenti, nondimeno

  probatur primo: ogni stella che osserva un'altra stella deve essere da questa osservata con identico ed efficace raggio, ma ciò non avviene nel caso dei raggi assunti nell'equatore secondo il modo del Magini e pertanto questi raggi non sono efficaci. Ora, la proposizione maggiore non può essere ricusata: i raggi invero sono distanze proporzionali fra due punti, ergo è irragionevole affermare, come dissi altrove, che il primo punto dista di più o di meno dal secondo, che il secondo dal primo, giacché la distanza fra due termini è correlativa, sicché entrambi distano parimenti l'uno dall'altro. Dimostriamo quindi la seconda proposizione: quando nel luogo di posizione di un dato astro, del Sole ad es., ascende il luogo del raggio assunto nell'equatore di un altro astro, sia esso Saturno, il Sole a sua volta deve osservare Saturno con uguale raggio nell'equatore; ora, giacché ciò non si produce, i raggi nell'equatore non si producono secondo un rapporto reciproco, ergo tale modo è discordante. Nella figura 3 ad es., posto che il Sole sia in sestile a Saturno nell'equatore, nondimeno il Sole non tocca Saturno con il proprio sestile assunto nell'equatore, né il di lui circolo di posizione. Il Sole infatti taglia l'equatore con il circolo del suo esagono nel punto g , il cui circolo di posizione è la linea gfh; il circolo di posizione di Saturno, al contrario, è Saturno-a-s.

  Dices: quanto tu affermi non ha alcuna importanza, poiché i raggi dell'astro che osserva, allorché incidono nel circolo di posizione di un altro astro, si diffondono nel circolo intiero e raggiungono il prorogatore medesimo; ora, può ben accadere che i raggi del prorogatore non tocchino il circolo di posizione della stella che osserva, ma non è necessario che il prorogatore guardi a sua volta la stella che l'osserva. Ciò è confermato, primo : non si hanno da misurare i raggi del prorogatore, giacché non hanno valore e non devono essere considerati; secundo : nel nostro caso presente può accadere una situazione simile a due stelle che non siano tra loro congiunte che parzialmente, in modo che l'una tocchi l'altra per la maggiore ampiezza della sua sfera attiva (sphaera virtutis), ma non sia toccata dall'altra per la minore ampiezza della sfera attiva della seconda.

  Respondeo: il raggio non è una semplice proiezione luminosa, se così fosse vi sarebbero infiniti raggi; ma proiezione luminosa in virtù di una distanza proporzionale, non misurata in qualsivoglia modo, ma direttamente e senza mediazione da stella a stella o a un luogo determinato con il quale abbia contatto nel corso del suo periodo. Mediante questi, o stella o luogo, vengono trasmesse e le sue qualità e i suoi influssi alle cose inferiori; mediante questi vengono assunte le distanze proporzionali medesime, le quali sono raggi efficaci. Invero, come sopra è stato dimostrato, i raggi sono parti proporzionali del moto e dell'influsso che gli astri portano a compimento dopo il contatto (quem efficiunt Astra post congressum) . In tal modo le stelle che si osservano l'un l'altra devono avere necessariamente un rapporto reciproco della loro distanza e due devono essere i termini della distanza proporzionale che è l'irraggiamento; di questi termini il destro non deve distare dal sinistro né più, né meno di quanto il sinistro disti dal destro, ma in modo uguale sotto ogni rispetto. Pertanto se i raggi fra le stelle altro non sono che le loro distanze proporzionali, non è sufficiente che i luoghi delle distanze concordino con i circoli di posizione delle stelle, ma è necessario che concordino con le stelle medesime, soprattutto se si considera che i raggi non possono diffondersi lungo i circoli di posizione, come dimostrerò a suo luogo. Ora, per quanto riguarda le ragioni da te addotte, la prima è falsa: in effetti il Sole e la Luna hanno in sè virtù - secondo la dottrina di Tolomeo - e di prorogatori e di promissori, in quanto si stima che abbiano assolutamente la facoltà sia di ricevere che di emettere raggi. E per quanto attiene alla seconda tua argomentazione, essa è contraddittoria: la sfera di attività che circonda le stelle segue la forza della luce loro e più questa luce è grande e in intensità e in estensione, più grande è la sfera attiva delle stelle medesime; invero ogni astro forma contatto radiale, anche quello la cui magnitudine apparente sia infima, anche se debole sia la virtù del raggio in ragione delle forze della stella.

  Secundo probatur conclusio: può accadere che il luogo del raggio nell'equatore disti 28 e più gradi in declinazione dall'astro che osserva e pertanto il luogo del raggio non può agire nell'astro che osserva, giacché, a causa della grande distanza, il corpo dell'astro non è toccato da quel raggio e colà non v'è contatto, non v'è familiarità, non v'è azione, non v'è passione. Nella figura 3 ad es. il punto c del sestile di Saturno dista dal Sole circa 14 gradi e non può quindi agire nel Sole.

  Dices: la virtù del raggio si diffonde per tutto il luogo o circolo di posizione fino al corpo dell'astro.

  Respondeo che questa è una vana finzione, giacché nulla si diffonde al di fuori della luce; ora, il luogo del raggio non ha luce alcuna, quindi non può diffondersi, ma di questo argomento tratteremo in seguito.

  Tertio: gli astri non generano raggi se non lungo la via dei loro moti; ora gli astri non si muovono lungo la linea equinoziale, se non soltanto rispetto alla terra allorché sono sulla linea equinoziale medesima; pertanto gli astri non producono raggi nell'equatore (se non quando ivi sono, ché allora generano raggi nel mondo). É così dimostrata la proposizione maggiore: i raggi sono distanze proporzionali degli astri, in virtù dell'intervallo precedente e seguente del moto.

  Quarto: se si producessero raggi nell'equatore, dovrebbero necessariamente prodursi anche le congiunzioni nell'equatore, ciò che invero avviene rarissimamente, ovvero solo quando le stelle si congiungono nei punti equinoziali, ergo etc.; si dimostra così la proposizione maggiore: in ogni genere di raggi, prima familiarità è la congiunzione; se pertanto gli astri non si congiungono in un supposto genere di familiarità, non producono neppure le rimanenti familiarità di raggi. In effetti nella congiunzione gli astri danno principio a nuove qualità, che poscia accrescono e decrescono tramite il moto e le distanze; ora, se nell'equatore non principiano tramite la congiunzione nuove qualità, non producono neppure lungo l'equatore medesimo nessun'altra distanza proporzionale. E inoltre, pur se talora si congiungono lungo l'equatore, non possono produrre distanze proporzionali, né generare raggi efficaci, in quanto non si muovono lungo la linea equinoziale.

  Quinto: i raggi nell'equatore non sono secondo natura, ma sono assunti a puro arbitrio umano, ergo etc. I raggi protratti in circolo circondano ogni cielo, ma i pianeti non ne illuminano ogni singola sua parte nel medesimo modo in cui illuminano il circolo dei segni e i paralleli, ove per contro producono, con il loro moto e influsso, distanze reali e naturali, al di là di ogni nostro arbitrio, le quali cose tutte le stelle non compiono nelle rimanenti regioni del cielo, ma sono escogitate dagli uomini, non in virtù del moto e dell'influsso delle stelle, ma con il solo compasso; non in base al rapporto della quantità compresa dal termine a quo al termine ad quem , non per la via reale del moto degli astri, ma a partire dagli astri stessi ed anche dal loro diametro e nondimeno non lungo la via sulla quale transitano i pianeti e ove pertanto nullo è il loro influsso.

  Dices: la proiezione della luce degli astri è il principio della determinazione dei loro raggi; ora la proiezione della luce giunge ad ogni luogo e ad ogni parte del cielo, ergo i raggi tracciati intorno a un cerchio sono reali e naturali, non posti dall'arbitrio umano.

  Respondeo che non è sufficiente, all'efficacia della familiarità dei raggi, la semplice emanazione luminosa; se fosse sufficiente, ogni proiezione luminosa, sia essa proporzionale o meno, sarebbe una familiarità efficace, ciò che è falso: invero ogni spazio in cui giunge la luce degli astri non ha, in quanto tale, la virtù di rendere efficaci i raggi, ma è necessario che si producano realmente nel cielo distanze proporzionali da parte degli astri medesimi, in virtù del moto e del susseguente effettivo irraggiamento che sempre avviene da un luogo ad un altro e che appare dappresso e senza interposizione dal corpo luminoso degli astri medesimi, non dalla proiezione della luce; inoltre lungo la via del loro moto, non al di fuori di essa, lungo luoghi ove giammai transitano e a cui giammai pervengono. D'altronde, già ricusai questa obiezione nel primo libro (15).

NOTE

1. influxus : il significato proprio di questo termine è "ciò che è costante", "stabile", in opposizione a ciò che è passeggero, fluxus. Come vocabolo astrologico appare già in Firmico Materno e traduce il termine greco aporroia.

2. primum mobile : è il decimo cielo, primum poiché è il più alto, mobile poiché compie una completa rotazione apparente nel corso delle 24 ore. Esso è puro circolo ideale ed è diviso nelle dodici porzioni o segni dello zodiaco.

3. passiones luminis : sono le affezioni o accidenti (passiones) che la luce degli astri mostra a noi in virtù dei suoi passus ovvero dell'incedere stesso dei corpi luminosi, il quale incedere è vero e apparente insieme e ha diversi modi: "per lunghezza universale intorno alla terra, e particolare nello Zodiaco: per lato e per declinazione; all'alto et al basso nelli eccentrici, andando retti e conversi intorno all'epiciclo, e per il moto della trepidazione. Con quai moti sempre mutano sito e modo d'influire..." (Placido Titi, Tocco di paragone... p. 45). Ma si veda per esteso CÏlestis Philosophia 1,14: "De motu locali siderum, et Passionibus, quae ipsum sequuntur", di prossima pubblicazione su queste pagine.

4. Se al tempo del Titi questa affermazione appare nuova, di fatto la teoria è ben documentata nell'astrologia classica.

5. Assumendo come obliquità dell'eclittica 23°31' - accettata dagli astronomi del XVI e XVII secolo - una stella posta sul circolo tropico invernale, ovvero all'inizio del Capricorno, avrà pertanto una declinazione di 23°31' e alla regione in cui il poli del mondo si eleva di 43° i suoi tempi orari diurni sono 11°00'36", che moltiplicati per 12 danno la quantità del suo arco diurno: 132°07'. Al contrario, posta una stella sul circolo tropico estivo, ovvero all'inizio del Cancro, mostrerà i predetti valori, ma complementari, rispettivamente di 15° e di 360°.

6. Non già nel Primum Mobile del Magini, ma forse nelle Tabulae novae iuxta Tychonis rationes elaboratae quibus Directionum conficiendarum brevior ac facilior quam unquam antehac a nemine ars traditur, Bononiae 1619, che non ho potuto consultare. Ma si confrontino altresì le varie introduzioni astrologiche dello stesso Magini nelle sue pubblicazioni di effemeridi (ad es. Ephemeridum cÏlestium motuum Io. Antonii Magini Patavini ab anno Domini 1598 usque ad annum 1610..., Venetiis 1599, p. 15: "Oppositio...noxius et malus maxime censetur ratione oppositionis, quoniam quae opponuntur, maximeque distant, maxime etiam sibi inimicantur").

7. Astrorum radii ad cardines, et domus accepti secundum proportionales distantias, seu partes arcuum diurnorum, et nocturnorum eorundem Siderum, sunt verae, et efficaces familiaritates, quas in Mundo voco. Si osservi che l'espressione in mundo non corrisponde alla greca (peri to kosmikon) bensì a formulazioni quali:.kata thn genesin, kata thn wran.

8. Sia ad es. la Luna a 13°53' Pesci, latitudine meridionale 4°35', declinazione 10°35'; latitudine della regione 43°. La sua ascensione retta è 346°56', il suo semiarco diurno 79°47'. Se sottraggo il suo semiarco diurno dalla sua ascensione retta, ottengo l'ascensione retta del meridiano allorché la Luna sorge all'oriente (267°09'). Se al contario aggiungo il suo semiarco diurno alla sua ascensione retta ottengo l'ascensione retta del meridiano all'atto del tramontare della Luna (66°43'). Entrambi i punti situati sul meridiano sono in quadrato con la Luna; infatti se dall'ascensione obliqua della Luna sottraggo 90 gradi, ottengo il punto culminante sulla linea ortiva della Luna: ascensione obliqua della Luna (= ascensione retta Luna + differenza ascensionale Luna) = 357°09' - 90° = 267°09'. E' questo il quadrato destro della Luna in mundo, (praecellentia) efficacissima. Il quadrato sinistro in mundo, che i Greci chiamano, (radiorum proiectio), si comprova non già a partire dall'ascensione (AO), ma dalla discensione obliqua (DO) della Luna e aggiungendo ad essa discensione i 90 gradi del quadrante: DO Luna 336°43' + 90° (-360°) = 66°43'.

9. L'autore allude al commento di Valentino Nabod al Quadripartitum di Tolomeo, di cui il Magini pubblicò brevi stralci, in particolare fa riferimento a carte 116b, 117a del De Astrologica ratione, ac usu dierum Criticorum, seu Decretorium... Venetiis 1607. Per coluro si intenda ogni circolo che passa per i poli del mondo, non solo il coluro equinoziale e solstiziale ("omnes coluri, seu circuli per mundi polos descripti sunt inter se ubique similes" V. Nabod apud Magini, op. cit., 116b). La rotazione diurna dell'equatore celeste è uniforme ed è fondamento del luogo simile (Tolomeo 3,10; p. 290 Robbins) cui si riferisce il commento del Nabod.

10. Tota regio orientalis adversatur occidentali... Ogni parte dell'oriente è quella che ascende all'orizzonte dall'emisfero invisibile, sia che essa coincida con il punto sorgente dell'eclittica o no, in altre parole: qualunque sia il suo azimuth. Nella figura 4 a, c, d, g sono sulla linea d'oriente, f,b,z,r, sulla linea di occidente e i primi sono opposti ai secondi, quantunque il diametro della loro opposizione non passi in ogni caso per il centro della sfera. Si consideri ad es. la posizione di un astro, sia esso la Luna, come dichiarato a nota 8, polo della regione 43°, grado eclittico che sorge all'oriente 25° Toro..
Vogliamo determinare in quali punti della linea d'orizzonte sorge l'oroscopo (25° Toro) ed è sorta la Luna. Cerchiamo in altri termini i loro azimuth, servendoci a tale scopo della più semplice formula: cos (az) = sin d/cos phi
otteniamo: azimuth Luna 104°13'; azimuth dell'oroscopo 63°27'. Ricordiamo che l'angolo dell'azimuth si misura lungo l'orizzonte da Nord verso Est. Nella figura a è il punto dell'orizzonte in cui sorge la Luna, b è il punto in cui sorge il grado dell'oroscopo. Si osservi che l'arco CD è l'amplitudine ortiva dello zodiaco (in altri termini del Sole ai punti estivi (C) ed invernali (D) ), l'arco EF la massima amplitudine ortiva della Luna, l'arco GH la massima amplitudine ortiva dell'astro di Venere.

11. Coelestis Philosophia 2,7 p. 180: " ogni significato attivo delle case proviene loro dai corpi luminosi, intendo dagli astri; abbiamo infatti mostrato altrove che cio che è privo di luce non può essere attivo, pertanto le case traggono dagli astri anche la determinazione della loro quantità. "

12. Questa forma del congiungersi è chiamata dal Titi coniunctio virtualis, in contrapposizione alla coniunctio praesentialis, la ; cfr. Coelestis Philosophia p. 150.

13. Sphaera activitatis è termine placidiano. Nella versione latina del Madkal al kabir di Abû Ma'shar (Introductorium in Astronomiam Albumasaris... Venetiis 1506 7,5) troviamo virtus corporis e anche vis luminis ; sono radii virtuales che gli astri circumcirca se potentes emittunt (L. Bellanti, De astrologica veritate...Florentiae 1495, 8,2), un'estensione dei raggi del corpo dell'astro che si propaga "en rond, c'est à dire tout au tour de leur corps" ( A. de Villon, De l'usage des ephemerides...Paris 1624, I,142) e che J.B. Morin de Villefranche chiamerà in seguito fortitudo intrinseca (Astrologia Gallica...Hagae Comitis 1656, 18,2) e vis fortitudinis (ibid. 16,13).

14. G.A. Magini espose il modo di determinare i raggi nell'equatore nel nono libro del sua esaustivo Primum mobile duodecim libris contentum in quibus habentur Trigonometria sphaericorum et Astronomica, Gnomonica, Geographicaque problemata ac praeterea Magnus Trigonometricus Canon emendatus et auctus ac Magna Primi Mobilis Tabula ad decades primorum scrupulorum supputata, Bononiae 1609, fo. 215 r-v. Ivi l'eccellente matematico propone la seguente formula (che diamo secondo il modo della moderna trigonometria):

Questa formula non può tuttavia servire alla determinazione del raggio quadrato; il coseno di tale raggio è infatti uguale a zero e il punto in cui tale raggio incide esprime sempre il punto che sorge (quadrato destro) o che si corica (quadrato sinistro) rispetto al luogo dell'astro da cui si misura il raggio. Pertanto il quadrato si calcolerà agevolmente aggiungendo o sottraendo all'ascensione retta dell'astro 90 gradi; il risultato sarà l'ascensione o la discensione obliqua del punto cercato. Si veda ad es. il calcolo della direzione aneretica escogitata dal Magini nella natività del cardinale Anton Maria Salviati (De Astrologica ratione ... cit., fo. 100 v)

15. Cfr. Coelestis ph. 1,14 p. 80s.: De motu locali siderum et passionibus quae ipsum sequuntur. Anni dopo, pubblicando il Titi le Tabulae primi mobilis, le faceva precedere da alcune tesi che riassumevano gli argomenti trattati nella Coelestis philosophia. Le tesi dal numero 38 al 41 concernono il presente capitolo e in esse l'autore porta a sostegno della sua argomentazione il cap. 4 dell'VIII libro dell'Almagesto, le prime parole del proemio al Quadripartitum, il penultimo capitolo del primo libro dello stesso, ove Tolomeo parla dell'esagono di Venere al Sole e infine il capitolo sulla durata della vita, già citato nel testo presente. Una dotta esposizione "placidiana" sul duplice moto si può leggere nel Lexicon di Gerolamo Vitali (edizione parigina) alla voce motus.