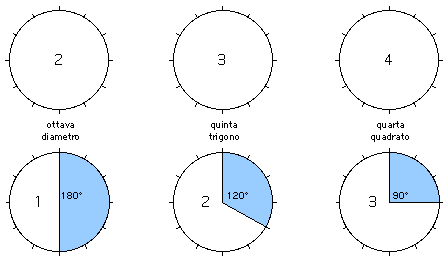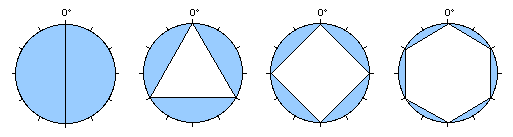L'argomento delle familiarità, ovvero dei rapporti che uniscono in qualche modo i segni dello zodiaco e i corpi celesti sarà trattato in più parti. Iniziamo per prima cosa a vedere su quali basi si fondano le relazioni più elementari tra i dodici segni.

Lo zodiaco come sistema musicale

  «La prima familiarità che intercorre tra le parti dello zodiaco è prodotta dalla mutua configurazione. Sono mutuamente configurate quelle parti che si trovano in una posizione diametrale, abbracciando due angoli retti ovvero sei segni o 180 gradi; quindi quelle che sono in posizione triangolare...». Così Tolemeo inizia il 13° capitolo del primo libro della Tetrabiblos, che tratta delle configurazioni tra i segni dello zodiaco. Il testo è riportato per intero alla fine di questa pagina.

  I rapporti che si creano in un circolo diviso in 12 parti uguali - come quello dello zodiaco - sono i medesimi che ritroviamo nella musica. Il circolo è assimilato alla doppia ottava, che contiene tutti i rapporti consonanti: quello di quarta (4/3), di quinta (3/2), di ottava (2/1), e di doppia ottava (4). Questi rapporti furono scoperti dai greci mediante esperimenti con corde di diversa lunghezza o con vasi riempiti d'acqua: facendo risuonare un vaso vuoto ed un vaso identico riempito d'acqua a metà si produce la consonanza dell'ottava; un vaso riempito fino a un terzo produce con il vaso vuoto la consonanza della quinta; riempito di un quarto la consonanza della quarta.

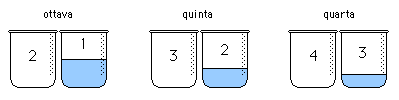
  Questi sono i rapporti consonanti maggiori: un accordo di ottava, di quinta o di quarta produce un'assimilazione dei suoni, una commistione che il musicista chiama crasi. Tolemeo, nel terzo libro del Manuale di Armonia, dimostra che gli stessi rapporti che generano le consonanze e le dissonanze musicali sono riscontrabili nel circolo diviso in 12 parti uguali, poiché 12 è il minimo comun denominatore delle frazioni 1/2, 1/3, 1/4 (vedi il capitolo intero in fondo alla pagina).

  Allo stesso modo dei rapporti musicali, i rapporti angolari di 180° (diametro od opposizione), 120° (trigono) e 90° (quadrato) assunti nel circolo intero sono "consonanti" e mettono in comunicazione i punti estremi: se due corpi celesti si trovano a queste distanze angolari tra loro le loro qualità luminose entrano in comunicazione e si produce una crasi, così come accade nei suoni. Alla base di questa teoria dell'emanazione luminosa sta una filosofia della natura secondo la quale la crescita delle forme naturali - sulla quale influisce la luce degli astri - avviene secondo proporzioni armoniche non dissimili da quelle dei suoni. Torneremo su questo argomento quando tratteremo degli aspetti tra gli astri.

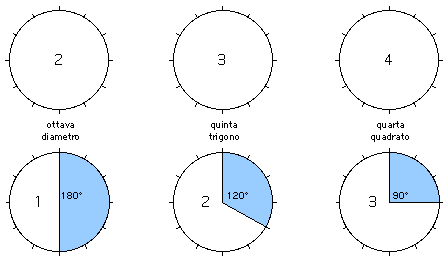
  A questi tre rapporti, il diametro, il trigono e il quadrato, se ne aggiungono altri due: la congiunzione (0°) che corrisponde all'unisono, e l'esagono o sestile (60°) che corrisponde al rapporto di 6/5. Quest'ultimo è generato per differenza tra il diametro e il trigono, mentre la differenza tra il diametro e il quadrato genera un altro quadrato:

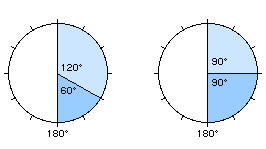
  Abbiamo dunque quattro rapporti (la congiunzione non è propriamente un rapporto ma un'identità di luogo), assunti per distanze angolari nel cerchio intero, e li chiameremo aspetti. Non considereremo altri aspetti angolari, sebbene molti ne siano stati enumerati, a partire da Keplero in poi.

	aspetto	distanza	rapporto	rapporto
	diametro (opposizione)	180°	12/6	2/1
	trigono	120°	12/8	3/2
	quadrato	90°	12/9	4/3
	esagono (sestile)	60°	12/10	6/5

  Il diametro divide il circolo in due emicicli, mentre il trigono, il quadrato e l'esagono, completando le rispettive figure, dividono il circolo in tre, quattro e sei settori:

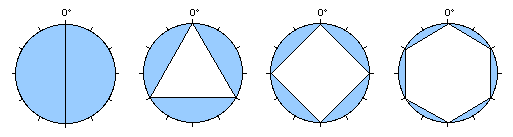
Aspetti angolari nello zodiaco

  Assumendo queste figure sul circolo zodiacale possiamo stabilire le prime relazioni tra i segni, considerati nella loro interezza: troveremo dunque segni tra loro in opposizione, in trigono, in quadrato, in esagono. La figura seguente mostra tutti gli aspetti angolari tra i segni: 6 diametri, 12 trigoni, 12 quadrati, 12 esagoni:

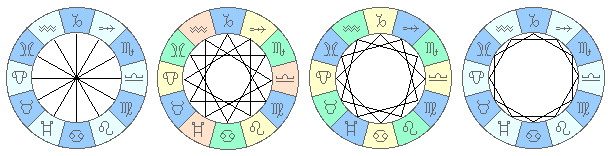
  Stabilite queste relazioni, possiamo notare che ciascun segno ha familiarità con 7 segni, mentre non ha questo tipo di familiarità con gli altri 4 segni. I segni che non hanno familiarità si chiamano incongiunti. Ciascun segno è incongiunto ai due segni ad esso contigui (che distano 30°) e ai due contigui al segno opposto (che distano 150°). Ad esempio l'Ariete non ha alcun aspetto angolare con il Toro, con i Pesci, con la Vergine, con lo Scorpione. Possiamo ora riassumere le familiarità e le incongiunzioni nella seguente tabella:

segni

  Vedremo nelle prossime lezioni che alcuni segni tra loro incongiunti per aspetto angolare, possono avere altri tipi di familiarità che si fondano su principî diversi.

Il testo di Tolemeo

  Tolemeo tratta delle familiarità tra i segni dello zodiaco nel tredicesimo capitolo del primo libro della Tetrabiblos. Ne riportiamo qui sotto la traduzione, così come faremo durante tutto il corso quando l'argomento trattato è presente nel testo tolemaico.

  Riteniamo utile riportare per intero il nono capitolo del III libro del Manuale di Armonia di Tolemeo. Queste considerazioni dell'astronomo alessandrino hanno grandissimo rilievo nell'arte astrologica.

Harm. III, 9 - Le consonanze e dissonanze del sistema musicale sono simili a quelle che troviamo nello zodiaco   Gli intervalli consonanti si dispongono entro un numero massimo di quattro parti, in quanto il maggiore, ovvero la doppia ottava, è espresso da una frazione il cui numeratore contiene quattro volte il denominatore e il minore, ovvero l'intervallo di quarta, è espresso da una frazione il cui numeratore supera di un quarto se stesso. Allo stesso modo si determinano nello zodiaco le posizioni ritenute consonanti ed efficaci, ovvero attraverso la partizione del cerchio in quattro parti.  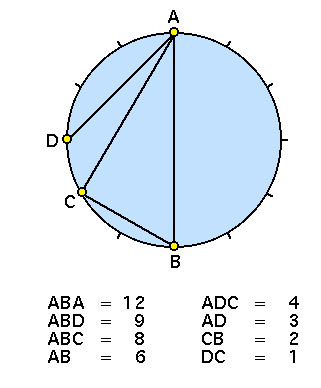Descriviamo il cerchio AB e dividiamolo a partire dal punto A in due parti uguali AB, in tre parti uguali AC, in quattro parti uguali CB. L'arco AB produrrà la posizione diametrale, l'arco AD la quadrata, l'arco AC la triangolare, l'arco CB l'esagonale. Ora, i rapporti degli archi di cerchio assunti dal medesimo punto A comprendono sia gli intervalli omofoni, sia i consonanti, sia l'intervallo del tono intero. Ciò sarà evidente se dividiamo il cerchio in dodici sezioni, in quanto 12 è il denominatore comune delle frazioni 1:2, 1:3, 3:4. Di queste sezioni, l'arco di cerchio ABD ne abbraccia 9, l'arco ABC 8, <l'arco AB 6,> l'arco ADC 4, l'arco AD 3. Le sezioni producono un rapporto di 2:1, che è il primo degli intervalli omofoni, ovvero l'ottava, in tre modi: le 12 sezioni del cerchio intero rispetto alle 6 dell'emiciclo, le 8 sezioni dell'arco ABC rispetto alle 4 dell'arco AC e le 6 sezioni dell'arco ACB rispetto alle 3 dell'arco AD.   Producono inoltre il rapporto sesquialtero [1 + 1/2], che è il maggior rapporto tra i primi intervalli consonanti, ovvero quello di quinta. Ed anch'esso in tre modi: le 12 sezioni del cerchio rispetto alle 8 dell'arco ABC, le 9 sezioni dell'arco ABD rispetto alle 6 dell'arco AB e le 6 dell'arco AB rispetto alle 4 dell'arco AC. Producono quindi il rapporto epitrito [1 + 1/3], che è il rapporto minore dei primi intervalli consonanti, ovvero quello di quarta. Ed anch'esso in tre modi: le 12 sezioni del cerchio intero rispetto alle 9 dell'arco ABD, le 8 dell'arco ABC rispetto alle 6 dell'arco AB e le 4 dell'arco AC rispetto alle 3 dell'arco AD. Producono poi un rapporto di 3:1, che è quello della consonanza dell'ottava e della quinta insieme, e ciò in due modi: le 12 sezioni del cerchio intero rispetto alle quattro dell'arco AC e le 9 dell'arco ABD rispetto alle 3 dell'arco AD. Producono in seguito un rapporto di 4:1, che è quello della doppia ottava, una volta soltanto: le 12 sezioni del cerchio intero rispetto alle 3 dell'arco AD. Producono ancora il rapporto di 8:3, che è quello della consonanza dell'ottava e della quarta insieme, una sola volta: le 8 sezioni dell'arco ABC rispetto alle 3 dell'arco AD. Producono infine il rapporto dell'epogdo [1 + 1/8], che è quello del tono, una volta soltanto: le 9 sezioni dell'arco ABD rispetto alle 8 dell'arco ABC. Fra queste relazioni, potremmo disporre la quinta, che è uno dei primi intervalli consonanti, secondo la posizione triangolare, l'intervallo di quarta secondo la posizione quadrata e il tono secondo il dodecatemorio. Infatti, il cerchio intero produce un rapporto di 2:1 rispetto all'emiciclo AB, e questo ha, rispetto all'arco AC del triangolo, un rapporto sesquialtero [1 + 1/2] e l'arco AC ha, rispetto all'arco AD del quadrato, un rapporto epitrito [1 + 1/3] e la loro differenza [AC-AD] è l'arco CD, che risponde al tono intero e comprende un dodecatemorio del cerchio. Pertanto, la natura ha costituito secondo una conveniente proporzione il circolo dei segni in dodici parti, poiché la doppia ottava è assai prossima al sistema compiuto di dodici toni e l'intervallo di un tono conviene a un dodicesimo del cerchio. È invero mirabile constatare che i punti separati da un solo dodecatemorio non sono consonanti nello zodiaco, ma solo nel genere melodico, mentre quelli che distano cinque dodecatemori mancano di un rapporto melodico. Sono per ciò chiamati incongiunti e sono solo in potenza. Infatti, consideriamo i due archi di cerchio prodotti da una corda che sottende un dodecatemorio: i rapporti che il cerchio intero produce saranno di 12:1 o 12:11, che sono estranei agli intervalli consonanti, ma non al genere melodico. Consideriamo poi i due archi di cerchio prodotti da una corda che sottende cinque dodecatemori: il cerchio intero produrrà rapporti di 12:5 o 12:7, estranei sia agli intervalli consonanti, sia ai melodici, in quanto non sono l'un l'altro né multipli, né parti aliquote, né composti da intervalli consonanti. Infine, da tutti i punti del cerchio che delimitano i dodecatemori si ottengono tre sole forme di quadrati, pari in numero alle specie dell'intervallo di quarta e solo quattro forme di triangoli, pari in numero alle specie degli intervalli di quinta, poiché solo questi intervalli sono, tra le consonanze, semplici.