Questo è un corso introduttivo di astrologia classica. Con il termine “classica” intendiamo quell’astrologia che ha mantenuto una unitarietà di principî e di linguaggio, dalla seconda metà del primo millennio a.C. fino al XVII secolo. Per fare un esempio, un astrologo del 1600 avrebbe ancora potuto capire qualcosa di questo testo di Vettio Valente scritto nel II sec. d.C.: «Se i paradidontes o i paralambanontes sono orientali e signoreggiano l’anno o i tempi generali e se nell’epembasis giungono ai luoghi operosi e hanno fase orientale, producono eventi chiari e salienti, giacché in tal modo la loro efficacia è suscitata, ed ogni astro produce ciò che è proprio alla sua natura». [Anth. IV.14]. Al contrario, per un astrologo del 1800 o del 1900 queste parole di Valente sarebbero risultate incomprensibili.

  Accettiamo dunque queste premesse generali:

• esiste un influsso degli astri sulle cose che accadono sulla Terra;
• questo influsso viene percepito in forme riconoscibili;
• l’influsso riconoscibile proviene dai corpi celesti che hanno una luce visibile dall’occhio dell’uomo;
• l’influsso dei corpi celesti luminosi si manifesta attraverso i loro moti apparenti e le variazioni dei loro cicli luminosi;
• l’influsso agisce sulla materia, sul corpo.

  Di conseguenza:

• accetteremo come produttori di influsso il Sole, la Luna, i pianeti fino a Saturno, le stelle, le comete, e tutti i fenomeni luminosi del cielo;
• per giudicare l’influsso dei corpi celesti dovremo innanzitutto saper misurare i loro moti rispetto alla Terra, ovvero dovremo conoscere i fondamenti dell’astronomia di posizione. L’astrologia infatti può definirsi come l’arte di giudicare mediante l’astronomia.
• i fondamenti astronomici riguardano tutti i fenomeni celesti percepibili dall’uomo: i moti degli astri, le condizioni della loro visibilità, il loro sorgere e tramontare, la qualità della loro luce, la durata dei loro cicli luminosi, e così via.
• i fondamenti astronomici riguardano solo i fenomeni apparenti, così come li vediamo dalla Terra. Per esempio, da questo punto di vista non ha alcuna importanza che la Terra ruoti attorno al Sole o che il Sole ruoti attorno alla Terra, poiché in entrambi i casi la nostra percezione del fenomeno rimane la stessa. Ciò che conta è unicamente la nostra percezione delle posizioni e dei moti dei corpi celesti rispetto al nostro punto di osservazione.

Alcune avvertenze per la parte matematica

• la parte matematica è particolarmente “corposa” nelle prime due lezioni, poiché per prima cosa occorre fornire la base astronomica sulla quale via via si costruirà la teoria astrologica: non vi è astrologia senza astronomia;
• non è richiesta tuttavia alcuna particolare “abilità” o inclinazione per la matematica. Occorre solo munirsi di una calcolatrice tascabile di tipo scientifico, con le funzioni trigonometriche e la trasformazione da decimali a sessagesimali e viceversa, ed eseguire esattamente le formule come spiegato.
• Alcune ottime calcolatrici "shareware" sono scaricabili da Internet:
  Per Windows consigliamo "Midget" una calcolatrice perfetta per il nostro corso, che permette di scrivere per esteso le formule con le parentesi e di visualizzare i risultati in gradi, minuti e secondi. Non si potrebbe immaginare di meglio. Si trova al sito: http://www.wrotniak.net/works/midget/. Ricordarsi di "settare" la calcolatrice in modalità "Deg" e non "Rad" come appare per default. Ricordarsi che sulla tastiera il tasto per la moltiplicazione è l’asterisco “*“.

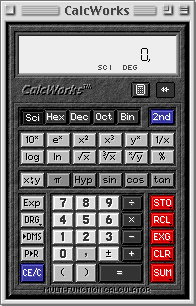
Per Macintosh è ottima “CalcWorks“ il cui uso è assolutamente identico a quello delle normali calcolatrici tascabili. Si può scaricare dal sito: http://brochusoftware.com/calcworks/. In questa calcolatrice i minuti e i secondi vanno inseriti di seguito dopo la virgola: per esempio 52°18’33" si scrive 52,1833 e poi con i tasti 2nd DMS (che diventa DEC) si ottiene la trasformazione in decimali: 52,3091666667.

• Il corso insegna anche l’uso di alcune tavole manuali che consentono spesso di operare senza calcolatrice, come si faceva una volta.
• i gradi sono talvolta riportati con la notazione sessagesimale, talvolta con quella decimale. Così ad esempio lo stesso dato può comparire come 319°23’45" (gradi, minuti, secondi) o come 319,395833 (gradi, decimali). Spesso sono riportati solo 3 decimali, che corrispondono ad una precisione di 3,6 secondi d’arco. Talvolta il numero dei decimali è superiore per permettere un controllo più completo delle operazioni sulla calcolatrice.
• le formule trigonometriche sono riportate con la consueta notazione matematica, dove le moltiplicazioni e le divisioni vengono risolte prima delle addizioni e delle sottrazioni, ovvero sen(a) cos(b) + cos(c) tan(d) significa (seno di a per coseno di b) + (coseno di c per tangente di d). Gli esempi numerici sono riportati con i simboli classici delle operazioni: 23 x 12 + 42 x 8 = 276 + 336 = 612. Il simbolo della divisione negli esempi numerici è "/", per evitare confusioni con il simbolo dei due punti ":".